Bucky
- 79
- 0
Homework Statement
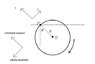
Uniform disc, mass m, falls from position where theta 60 degrees. (P is a fixed point on rim of disc).
Calculate the components of thrust along and perpendicular to GP on the smooth hinge at P when theta = 30degrees.
see attatched image for diagram
Homework Equations
The Attempt at a Solution
NB: theta with a dot is velocity (v), and theta with two dots is acceleration (r). Not sure if these are actually what the two of them mean, but that's what they'll be represented by.
Transverse Equation:
-ma(r)= mg sin theta - x
x = mgsin theta + ma(r) (1)
Radial Equation
ma (v)^2= y - mgcos theta
Y = ma (v)^2+ mgcos theta (2)
Rotational equation about P
I r= sum of moments
2/3 m(a)^2 r= -mgasin theta
2/3a r= -g sin theta
a r= -(3/2) g sin theta (3)
Integrating (3) gives
a r= -3/2g cos theta + c
c = 3/2g cos theta
at theta = 60
c = 3/2g cos 60
therefore
c = 3/4 g
so
a (v)^2= -3/2g cos theta + 3/4 g
at theta = 30, (3) gives
a r= -3/2g sin30
= -3/4g
(4) gives
a (v)^2= -3/2g cos30 + 3/4g
= -3/2 * root(3)/2g + 3/4g
= -3root(3)/4g + 3/4g
= (3-3root(3))/4 g
From (3), at theta = 60
-ma r= mgsin theta - x
-m(-g/3) = mgsin60 - x
1/3mg = root(3)/2mg - x
1/3mg = root(3)/2mg - x
2/6mg = 3root(3)/6mg - x
x = 3root(3) - 2/6 mg
which is wrong. So I won't even bother looking at my value for y...
And I'm not sure where I've went wrong :/ seems every time i attempt this question I get a different answer.