Solve Rotational Dynamics Homework: Hollow Cylinder, Weight, String

[golanor]

Homework Statement

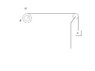
A hollow cylinder of internal radius r and external radius R and mass M is connected by a string to a weight m.
What are the angular and linear acceleration of the cylinder? Assume that the cylinder is rolling without slipping.
What is the acceleration of the weight and what is the tension on the string?

Homework Equations

*everything*

The Attempt at a Solution

First, by using dimensional analysis i can see that the solution should be something along the lines of:
a=\frac{m*r}{M*R}g
I tried to do Newton's second law, for the cylinder i get that:
\sum F=T=\text{Ma}
torque:
\sum \tau =T*R=\text{I$\alpha $}
moment of inertia around the center of mass:
I=M\left(R^2-r^2\right)
and the relation between the angular and linear acceleration:
\alpha =\frac{a}{r}

I have no idea what i did wrong or what do i need to do next.
Thanks in advance!

 

[haruspex]

Because the cylinder is rolling, you need to be a bit careful about the moments. If you take moments about the centre of mass of the cylinder then you have to include the torque from friction at the point of contact. Alternatively, you can take moments about the point of contact and use the parallel axis theorem for the moment of inertia.
You've left friction out of the linear acceleration equation for the cylinder.
You also need a linear acceleration equation for the mass m.

 

[golanor]

Because the cylinder is rolling, you need to be a bit careful about the moments. If you take moments about the centre of mass of the cylinder then you have to include the torque from friction at the point of contact. Alternatively, you can take moments about the point of contact and use the parallel axis theorem for the moment of inertia.
You've left friction out of the linear acceleration equation for the cylinder.
You also need a linear acceleration equation for the mass m.

\sum F=m*g-T=m*a

Shouldn't the friction be 0, since the cylinder is rolling without slipping?

 

[haruspex]

\sum F=m*g-T=m*a

Yes.

Shouldn't the friction be 0, since the cylinder is rolling without slipping?

If the friction is zero it's sure to slip. 'Rolling' tells you that static friction is enough to prevent slipping.

 

[golanor]

I tried to do Newton's second law, for the cylinder i get that:
\sum F=T=\text{Ma}
torque:
\sum \tau =T*R=\text{I$\alpha $}
moment of inertia around the center of mass:
I=M\left(R^2-r^2\right)

If the friction is zero it's sure to slip. 'Rolling' tells you that static friction is enough to prevent slipping.

I understand..just got confused by something we proved in class.
So, the linear acceleration should be: \sum F=T-f=M*a_1
and the torque around the center of mass: \sum \tau =R(T+f)=\text{I$\alpha $}
Around the point of contact: \sum \tau =2R*T=\text{I$\alpha $}
And in this case, the moment of inertia will be I=M\left(R^2-r^2\right)+M\left(R^2\right)

 

[haruspex]

And in this case, the moment of inertia will be I=M\left(R^2-r^2\right)+M\left(R^2\right)

A couple of problems with the first term on the RHS there. What would the MI be about the cylinder's centre if r were only a little less than R?

 

[golanor]

A couple of problems with the first term on the RHS there. What would the MI be about the cylinder's centre if r were only a little less than R?

Well, i forgot the 1/2 there. it's basically the MI of the large cylinder minus the one we took out. They are co-centric so there is no distance to add. if i look at extreme cases - r<<R it's as if the cylinder is complete, r=R - there is no mass. = the equation makes sense.
I=\frac{1}{2}M(2R^{2}-r^{2}) - this is relative to the contact point.
i know it's wrong tho, since when i put it into the equation i get r^{2}=0
the thing is, i don't know what I'm doing wrong.

 

[MrWarlock616]

it's basically the MI of the large cylinder minus the one we took out.

How do you know the mass of the cylinder you took out is the equal to the mass of the original cylinder?

 

[golanor]

How do you know the mass of the cylinder you took out is the equal to the mass of the original cylinder?

They have the same density.
I=\rho \left(\int _0^h\int _0^{2\pi }\int _0^Rr^3drd\phi dz+\int _0^h\int _0^{2\pi }\int _0^rr^3drd\phi dz\right)=\frac{M}{\pi *h\left(R^2-r^2\right)}h*\frac{\pi }{2}\left(R^4-r^4\right)=\frac{M}{2}\left(R^2+r^2\right)

 

[haruspex]

They have the same density.
I=\frac{M}{2}\left(R^2+r^2\right)

That's better. (And of course +MR² for parallel axis.)

 

[golanor]

The point I missed was the relation between the cylinder's acceleration and the weight's acceleration.