Solve Statics Problem: Find Theta Angle Balance

[Ortix]

I basically have to solve the system below for which angle theta it's in balance. Meaning all forces equal out to 0. The answer is in terms of the variables.

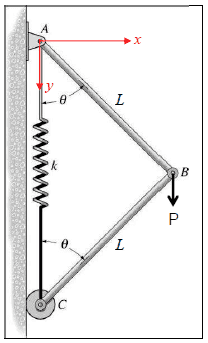
It's been a while since I've done statics like this but it has come back to bite me in the *** again.

I started out by moments about A:
2L*cos(θ)*Cx - P*L*sin(θ)

But now what? If I do sum of forces in X I get that Ax = Cx and then I get stuck with the sum of forces in Y

Do I have to make a cut somewhere? Not sure about to go about solving with the spring.

The answer is:
cos(θ) = 0.5*(1+(P/2kL))

Any ideas?

 

[mfb]

At C, there is an unknown horizontal force C<->wall, a vertical force (depends on the position of C only via the spring) and an unknown force along BC. You can relate theta to the position of C, and that allows to determine the two unknown forces.
Consider the equlibrium at B to relate the force in the lower arm to the force in the upper arm. That might be sufficient to solve the problem, otherwise consider forces at A.

 

[Ortix]

with the unknown force along BC do you mean the normal force inside the beam?

 

[haruspex]

with the unknown force along BC do you mean the normal force inside the beam?

The compression force in the beam. Note that because of the free joints at each end, there can be no torque passed through the beam.