mrlucky0
- 69
- 1
[SOLVED] Tension in a Line
A rope is fixed at both ends on two trees, and a bag is hung in the middle of the rope, causing the rope to sag vertically. If the tree separation is 10 m, the mass of the bag is 5.0 kg, and the sag is 0.2 m, what is the tension in the line?
I drew a free body diagram and determine that the angle of the sag was about 5.7 degrees. I'm not to sure where to go from here. Any help would be appreciated.
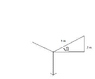
Edit: I've attached the free-body diagram. Here I focus on half of the rope which I assume to be 5 m.
Homework Statement
A rope is fixed at both ends on two trees, and a bag is hung in the middle of the rope, causing the rope to sag vertically. If the tree separation is 10 m, the mass of the bag is 5.0 kg, and the sag is 0.2 m, what is the tension in the line?
Homework Equations
The Attempt at a Solution
I drew a free body diagram and determine that the angle of the sag was about 5.7 degrees. I'm not to sure where to go from here. Any help would be appreciated.
Edit: I've attached the free-body diagram. Here I focus on half of the rope which I assume to be 5 m.
Attachments
Last edited: