Solve the Superbowl Public Works Problem with a Binary Circuit | Homework Guide

[Blues_MTA]

Homework Statement

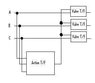
Using AND, OR, NOT, NAND, NOR gates construct a circuit for the following problem

7. One of the more interesting public works problems is the “Superbowl” problem. At
the beginning of halftime during the Superbowl, 35 million toilets are flushed almost
simultaneously. The resulting loss of water pressure wreaks havoc on many
municipal water systems. Here you will solve the problem for a “three toilet” system.
Devise a logic circuit whose “1” inputs represent “flushes” and whose “1” outputs
represent opened water-feed valves. If no more than one toilet is flushed, that toilet’s
water valve opens, and the others remain closed. If more than one toilet is flushed,
all the water valves remain closed.

Homework Equations

I Made a table of Values, but i have been banging my head against my desk for now designing various circuits, here is the link to the circuit builder

http://www.jhu.edu/~virtlab/logic/logic.htm"

Here is the Table that i came up with

IN OUT
001 001
010 010
011 000
100 100
101 000
110 000
111 000
000 000

Any Help is GREATLY Appreciated, thank you so much!

The Attempt at a Solution

 

[Zryn]

How about if you interpret the problem differently. Think of taking in 3 inputs to determine whether 1 action happens or not, and then combining whether 1 action happens or not with each of the 3 inputs, to determine which output the action is happening to?

Do you have a maximum number of gates allowed?

 

[Blues_MTA]

Wow, thanks for the insight, ill give that a try, I've been working on it for hours so I am a little exhausted at this point, thank you very much, any other advice is greatly appreciated

There are no limits as to how many gates we can use, just three input, three output

 

[Zryn]

One issue that may arise would be caused by propagation delays between input and output, depending on how fast things need to react.

If the inputs A B & C in the picture are one set of values and then they change to a different set, there may be a memory effect for a short period of time, where the new set of inputs get to the 'Valve T/F' decision box and the old set's 'Action T/F' outcome has not updated yet.

This can be fixed by figuring out the delay times through each gate in the 'Action T/F' box and then putting a 'Delay' box on each of the A B & C lines composed of multiple pairs of NOT gates. This will do nothing to the signal except add a delay between the input and 'Valve T/F' box, which is a cheesy way of fixing the problem, but sometimes works ;)