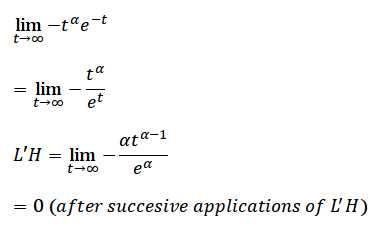Solving a limit with L'H's rule

  • Thread starter Thread starter Turion
  • Start date Start date
  • Tags Tags
    Limit
Turion
Messages
145
Reaction score
2

Homework Statement



OErDOT2.png


Homework Equations


The Attempt at a Solution



YG1M1Fh.png


Are you allowed to do that where you just apply L'H an infinite amount of times?
 
Physics news on Phys.org
Turion said:

Homework Statement



OErDOT2.png


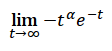
Homework Equations





The Attempt at a Solution



YG1M1Fh.png

After taking the derivative of the denominator, you should get et, not eα. I suspect that was a typo.

Anyway, your limit is correct. The basic idea is that power functions, such as tα grow large, but exponential functions grow large faster.
 

Thread 'Prove that the integral is equal to ##\pi^2/8##'

Prove $$\int\limits_0^{\sqrt2/4}\frac{1}{\sqrt{x-x^2}}\arcsin\sqrt{\frac{(x-1)\left(x-1+x\sqrt{9-16x}\right)}{1-2x}} \, \mathrm dx = \frac{\pi^2}{8}.$$ Let $$I = \int\limits_0^{\sqrt 2 / 4}\frac{1}{\sqrt{x-x^2}}\arcsin\sqrt{\frac{(x-1)\left(x-1+x\sqrt{9-16x}\right)}{1-2x}} \, \mathrm dx. \tag{1}$$ The representation integral of ##\arcsin## is $$\arcsin u = \int\limits_{0}^{1} \frac{\mathrm dt}{\sqrt{1-t^2}}, \qquad 0 \leqslant u \leqslant 1.$$ Plugging identity above into ##(1)## with ##u...
View full post »

Similar threads

Finding the Limit of x*sin(1/x) using L'Hopital's Rule
Replies
6
Views
2K
MHB 1.6.1 AP Calculus Exam Limits with L'H
Replies
3
Views
2K
MHB Limit $\frac{f(x)}{g(x)}$: Solve w/ L'H Rule
Replies
4
Views
2K
Which grows faster, (x-4)^3 or
Replies
13
Views
5K
Limit where l'Hopital's rule doesn't help
Replies
5
Views
2K
MHB What is the limit of a complex fraction with L'Hopital's rule?
Replies
1
Views
859
Help with understanding of L'Hospitals Rule
Replies
3
Views
2K
Violation of L'Hopital's Rule in Simplifying Rational Functions
Replies
8
Views
2K
Finding the limit of x/sqrt(x^2 + 1) as x--> +infty
Replies
4
Views
6K
What is the Limit of t raised to the Power of 1/t as t Approaches Infinity?
Replies
9
Views
2K

Hot Threads

Recent Insights

Back
Top