Ejayrazz
- 1
- 0
Perchance someone here has some background in Philosophy, specifically symbolic logic? For the life of me I can't figure out the following:
A v D
(~B ^ ~C) = D
B => ~(C=> A)
~B
What I have so far is this:
1| A v D ......P
2| (~B ^ ~C) = D ....P
3| B => ~(C =>A) ...P
4| |B ......A
5| | |C .......A
r| | |?
s| | |?
t| | |?
u| | |?
v| | |A ........1, ?-?, ?-?, vE
w| | C=>A ......5-v, =>I
x| | B => ~(C =>A) ...2, R
y| | ~(C =>A) .....w, x, =>E
z| ~B ......4, w, y, ~I
What I can't figure out is how to get the disjunction elimination for A in the second sub-derivation. Anyone have a clue?
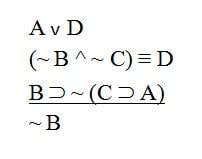
A v D
(~B ^ ~C) = D
B => ~(C=> A)
~B
What I have so far is this:
1| A v D ......P
2| (~B ^ ~C) = D ....P
3| B => ~(C =>A) ...P
4| |B ......A
5| | |C .......A
r| | |?
s| | |?
t| | |?
u| | |?
v| | |A ........1, ?-?, ?-?, vE
w| | C=>A ......5-v, =>I
x| | B => ~(C =>A) ...2, R
y| | ~(C =>A) .....w, x, =>E
z| ~B ......4, w, y, ~I
What I can't figure out is how to get the disjunction elimination for A in the second sub-derivation. Anyone have a clue?