mhirschb
- 3
- 0
I feel silly but I've been looking at this equation for a while and I don't fully understand the individual steps taken to go from the top line to the bottom line:
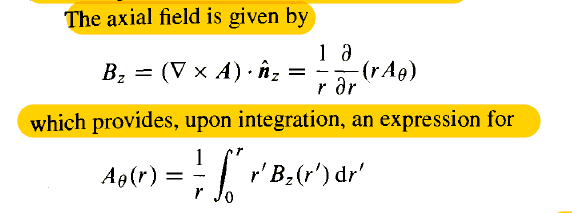
I think I am getting caught up with all the r's in the equation. I recognize that on the second line "r" describes the point at which we are evaluating the MVP, and r' is the domain of r that we're integrating over.
I'm confused because it looks like they've taken the 1/r and changed it to r' on the other side.
I think I am getting caught up with all the r's in the equation. I recognize that on the second line "r" describes the point at which we are evaluating the MVP, and r' is the domain of r that we're integrating over.
I'm confused because it looks like they've taken the 1/r and changed it to r' on the other side.