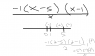PhysicsAdvice
- 37
- 0
Revenue Equation: R(x)=-x^2+10x Cost Equation: C(x)= 4X+5
Average profit= profit equation, P(x)/x
therefore p(x)= R(x)-C(x)=-x^2+6x-5
(-x^2+6x-5)/x=(-1(x-5)(x-1))/x, I then found that x is positive between 1 and 5, therefore average profit is positive in that range, however, the answer is if x>5, where did I go wrong?
(Picture illustrates the steps not shown)
Average profit= profit equation, P(x)/x
therefore p(x)= R(x)-C(x)=-x^2+6x-5
(-x^2+6x-5)/x=(-1(x-5)(x-1))/x, I then found that x is positive between 1 and 5, therefore average profit is positive in that range, however, the answer is if x>5, where did I go wrong?
(Picture illustrates the steps not shown)