Solving Bobbin on Incline: Angle of Tilt θ

[wwshr87]

Homework Statement

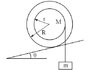
A bobbin of M = 3 kg consists of a central cylinder of radius r = 5 cm and two end plates of radius R = 6 cm. It is placed on a slotted incline on which it will roll but not slip, and a mass m = 4.5 kg is suspended from a cord wound around the bobbin. It is observed that the system is in static equilibrium. What is the angle of tilt θ of the incline?

Homework Equations

F=ma
Torque is force times arm perpendicular to the force.

The Attempt at a Solution

I know the torque being exerted by mass m is the force (mg) times the distance r; t=mgr.
This torque must be equal to the torque being exerted by the mass. How do I find that torque?

 

[tvavanasd]

How about a free body diagram of the bobbin, and your equations of static equilibrium?
Include the reactions of the ramp on the bobbin.

 

[Swap]

tvavanasd is right. U need to draw a free body diagram. And since it will roll on the incline u must take into account of the frictional forces.
for translational equilibrium the required equation will be
(M+m)gsinθ= µ(M+m)gcosθ...(1)
For rotational equilibrium the equation is
mgr=µ(M+m)gRcosθ...(2)
Divide equation 1 by 2 and u will get ur answer.