Solving Circular Motion Problems: Displacement, Speed, & Acceleration

[snagglepuffin]

Homework Statement

I do not know if this is the correct forum to post this in but here goes. I got all of the answers correct, but I just have a question on part F.

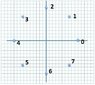
1.) The figure shows a motion diagram
of a particle in circular motion at a
constant speed. The axes have units
of meters. Each dot represents a 5
second time interval.

a) Write out the displacement
vector from point 1 to point 2 in
component form

b) Write out the displacement vector from point 1 to point 2 as a magnitude and
angle from horizontal.

c) What is the speed of the particle? To do this, determine a velocity vector and
take its magnitude.

d) Use graphical vector addition to show the direction of the acceleration at points 1
and 3. You can do this right on the figure or on another sheet of paper.

e) From your answer in part d, find the magnitude of the acceleration at point 3.
Remember a = ΔV/Δt

f) Compare your answer from part e to the result from a_radial = v²_tan/r

The Attempt at a Solution

Just to show you that I actually did the work, here are the answers I got.

A) -7i+3j

B) 7.61m at 23.2° above the -x axis.

C) 1.52 m/s

D) I drew the acceleration vector on my paper.

E) 0.226 m/s/s

F) 0.231 m/s/s

My question to you is why are the answers for Part E and Part F different? They are both correct (as calculated in the problems) and both describe the magnitude of the same acceleration vector.

Any and all help would be appreciated!

 

[Bandersnatch]

The difference comes from the fact that the 8 points are just an apporximation of a circle.

Try doing the same exercise with all the odd-numbered points removed(a worse appoximation of a circle), and then with twice as many as points as in the problem(a better approximation).
In the fromer case, you'll find out that the acceleration diverges even more, in the latter that it's closer to what you get from the equation in f.
Once you include infinite number of points to form the actual circle, your results will converge(integral calculus deals with this kind of infinite addition problems).

Think of what is the difference between the displacement you've been calculating, and the actual distance the point traveling in circular motion needs to cover. How does the difference affect velocity and acceleration?

 

[snagglepuffin]

Thank you Bandersnatch! That is what I was thinking. I re-evaluated it with more points and it was more accurate.