Dieinhell100
- 13
- 0
Homework Statement
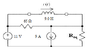
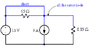
For t<0, the circuit shown below with the voltage source at 11 volts and three resistors combined into an equivalent, Req. We need to find the Thevenin equivalent circuit for the part of the circuit connected to the inductor.
First find Req, by combining series and parallel resistors.
Req = ? Ω. (I already solved it)
Find the Thevenin resistance across the inductor and the short circuit current.
Rt = ? Ω. (I already solved for it)
Isc = ? A. (This is what I don't have)
Homework Equations
Isc = Voc / Rt (Thevenin/Norton Theorem)
The Attempt at a Solution
The solved values I got (which are correct) for the resistances are:
Req= 8.89 Ω
Rt= 7.82 Ω
I got Rt from 1/Rt= (1/Req) + (1/65)
I've tried multiple times to solve for Isc. I think I mainly have a problem getting Voc or just combining voltage and current sources. I am attaching a picture of the circuit.
How do I get Isc?