ricky123
- 2
- 0
The potential on the side and the bottom of the cylinder is zero, while the top has a potential V_0. We want to find the potential outside the cylinder.
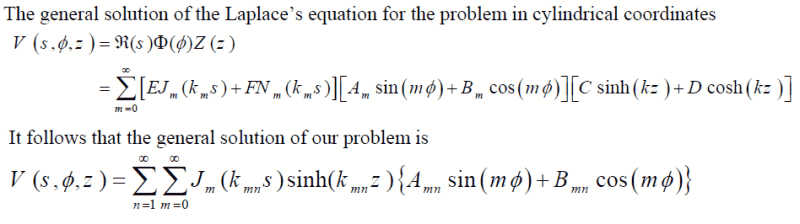
Can I use the same boundary conditions as for case of inside cylinder potential?
What is different?
Can I use the same boundary conditions as for case of inside cylinder potential?
What is different?