Oshada
- 40
- 0
ϵ-N proof
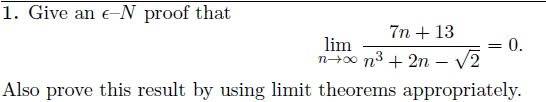
I've tried to make the denominator smaller as is usual with ϵ-N proofs. But the sqrt(2) confuses me. Any help is much appreciated.
Homework Statement
Homework Equations
The Attempt at a Solution
I've tried to make the denominator smaller as is usual with ϵ-N proofs. But the sqrt(2) confuses me. Any help is much appreciated.