Solving Oblique Triangles w/o Law of Sines/Cosines

[KC60523]

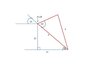
I need help solving for any other information about the red triangle. Due to the extremely limited information I already have, I can't use the Law of Sines (the angle is obtuse) or the Law of Cosines (gives no solution or non-real solutions for the information given) like I normally would. I only know the variables listed in the diagram. Is there any other way to get either the missing side or the other two angles? It has been a long time since I had geometry, so I'm hoping I'm just forgetting something simple.

Other information: a > b

 

[SteamKing]

The law of sines works for obtuse and acute angles.
See: http://en.wikipedia.org/wiki/Law_of_sines

For solutions to triangles: http://en.wikipedia.org/wiki/Solution_of_triangles

If you know the values of a and b and the angle θ2, you should be able to solve the red triangle. It will take several steps, but a solution should be readily obtained.

If you have further problems, provide explicit information and we can go through it step by step.

 

[janhaa]

Why can't you use Law of Sine? If you are naming top angle (to right) for $$\theta_3$$then ,
$$\frac{\sin(\theta_3)}{a}=\frac{\sin(\theta_2)}{b}$$
and the last angle
$$\theta_4=180^o-(\theta_2+\theta_3)$$
and finally the last side:
$$c^2=a^2+b^2-2ab\cos(\theta_4)$$

 

[verty]

For me, using the Law of Cosines to get the third side is the obvious first step. I don't see why it should fail. It may give you two answers because this is the ambiguous case, but you just choose the one you know is correct.

If it happens that the answer is nonreal, then I think b is too short for the triangle to exist with that angle.