Epiclightning
- 26
- 2
Homework Statement
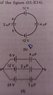
Find the potential difference between points a & b. Diagrams attached below. I have doubts in part (b) and (c).
Homework Equations
Q = CV, kirchhoff's laws
The Attempt at a Solution
I honestly don't get how the current can flow in opposite directions in part(b). if we choose the conventional notation, then the current flows out of both positive terminals and both intersect?? If not, how can we let the current flow out of the positive terminal in one battery and out of the negative terminal in the other?
In part (c), I'm confused as to how current could flow through that bridge in the middle. If we look at current coming out of the battery on the left, it will flow up the bridge. If we look at current flowing out of the right battery, it will flow down the bridge. This is contradictory, and if I change the direction of the current, I'm messing up the conventions again.

 giving it as a rational number, Vb = 3×24/7 so then we are able to see that the charges add up exactly, not just approximately and so plausibly exactly, to 0.
giving it as a rational number, Vb = 3×24/7 so then we are able to see that the charges add up exactly, not just approximately and so plausibly exactly, to 0.