Solving Space Junk Momentum Problem

[quickclick330]

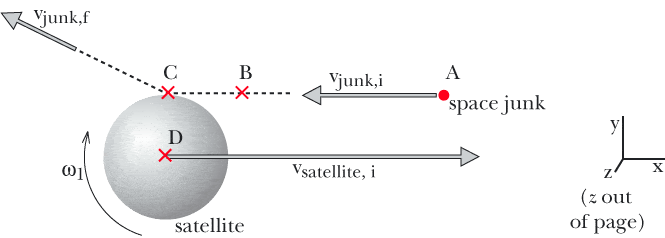
A spherical satellite of radius 4.7 m and mass M = 195 kg is originally moving with velocity = < 2700, 0, 0 > m/s, and is originally rotating with an angular speed = 2 radians/second, in the direction shown in the diagram. A small piece of space junk of mass m = 4.1 kg is initially moving toward the satellite with velocity= < -2100, 0, 0 > m/s. The space junk hits the edge of the satellite at location C as shown in the diagram, and moves off with a new velocity = < -1200, 490, 0 > m/s. Both before and after the collision, the rotation of the space junk is negligible.

MOMENTUM
After the collision, what is the final momentum of the satellite?

i tried this...

system: junk and satellite

so pf = pi

pjunk-f + psat-f = pjunk-i + psat-i

psat-f = (pjunk-i + psat-i)/ pjunk-f
= ((mjunk*vjunk-i) + (msat*vsat-i))/ (mjunk*vjunk-f)

= ((4.1 kg *<-2100,0,0> m/s) + (195 kg * <2700, 0 0> m/s))/ (<-1200, 490,0> m/s * 4.1 kg)

= <-437, 0 , 0>what am i missing/doing wrong? thanks!

 

[rl.bhat]

Here you have to use conservation of momentum and energy. You can wright three equations.
1) MsVsi -MjVji = MsVsf*cos(theta1) - MjVjf*cos(theta2){ x-components of momentums]
2) MsVsf*sin(theta1) = MjVjf*sin(theta2) [y-components of momentums]
3) 1/2*MsVsi^2 + 1/2*Is*wsi^2 + 1/2*MjVji^2 = 1/2*MsVsf^2 + 1/2*Is*wf^2 +1/2*MjVjf^2. [ conservation of energy]
In this we know Ms, Mj, Vsi , Vji , wsi and (theta2). Now we have to find Vsf, Vjf, Wsf and (theta1). Can you try further?

 

[rl.bhat]

Are you not interested in this problem? Realy it is a very good porblem. If you find it difficult to do all these calculations at a stretch, do in steps. If you stuck up take help.