Solving Stress Concentration for Elliptical Hole in Square Panel

[raunakm]

Homework Statement

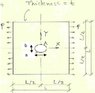
Square panel , elliptical hole, uniform pressure p in x direction. calc stress at end of minor axis. pt A

L=40in p=10psi a=1in b=0.5 in t=0.2 in

Homework Equations

i know that stress at end will be max stress multiplied by stress conc. factor.
bt i don't know how to calc stress conc. factor for an elliptical hole

The Attempt at a Solution

Kt = stress x (1 + 2b/a)

is this correct?

 

[mgb_phys]

Can't read the diagram but it's normally 1+2(a/b) where a is the length and b is the width.
So as the width gets smaller or the length is longer - the concentration gets bigger!

Alternatively it's sqrt(crack_length/radius)