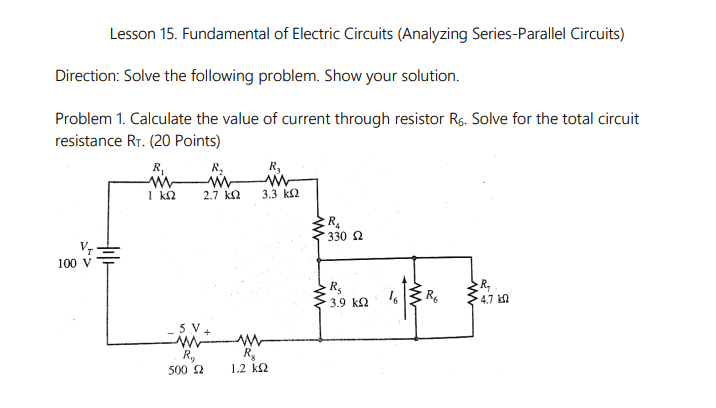
Discussion Overview
The discussion revolves around finding the missing resistor (R6) in a parallel circuit, focusing on the methods to calculate its value based on given current and voltage information. Participants explore various approaches to solve the problem, including the use of series and parallel resistor combinations.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant suggests that the current flow in the parallel circuit can be used to find the resistance of R6 but feels there is missing information.
- Another participant describes the problem as a straightforward series-parallel resistor combination and requests the original poster's work for clarity.
- A participant notes that the voltage across R9 is provided, which should offer enough information to solve for R6.
- One participant explains their approach of adding resistances in the series circuit to find current and then using that current to solve for R6, estimating a current of 0.01 A.
- Another participant confirms the current of 0.01 A and suggests writing an equation to solve for R6 while leaving it undefined.
- A participant expresses doubt about the previous calculations, stating that the total current of the parallel circuit must be 0.01 A, leading to a calculated total resistance of 10,000 ohms.
- Another participant challenges the idea of obtaining a combined parallel resistance greater than the smallest individual parallel resistor, asserting it must be no more than 3.9 kΩ.
Areas of Agreement / Disagreement
Participants express differing views on the methods to calculate the missing resistor, with some agreeing on the current value of 0.01 A while others challenge the implications of that value on the total resistance of the circuit. The discussion remains unresolved with multiple competing views on the calculations and approaches.
Contextual Notes
Participants reference specific resistor values and configurations but do not clarify all assumptions or dependencies in their calculations. The discussion includes unresolved mathematical steps and varying interpretations of the circuit's behavior.