slicer4ever
- 5
- 0
hey good people, I'm having a problem with how to solve a problem I'm having.
first of all, I am working on an isometric game, and align my tile's are layed out like so:
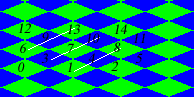
so, here's the problem:
the numbers are arranged in how the tile's are layed out in memory, however, i want to be able to get a patch of tile's relative to how the white lines are layed out.
for example: column 1 is 6, 9, and 13. 2 is 3, 7, and 10, and 3 is 1, 4, and 8.
so my input would be something like this: the bottom tile's index in the world(in this case that is tile #6), and then i'd specify which tile i was last on, and finally i'd pass the column and row size to get the chunk of.
the goal is to quickly determine which column/row the last tile is on, increment first by column, then by row. so i'd iterate over tiles 6, 9, 13, 3, 7, 10, 1, 4, and 8.
so, I've figured out how to specify a tile index, and get it's column/row with the following formula:
however, i also need to be able to input the column/row and get the tile index(or at least the x/y).
this is the math I've tried to do, but it's obviously not correct:
as you can see that doesn't work. however, after inputing the equations into wolfam:
http://www.wolframalpha.com/input/?i=%28x%2Bfloor%28h%2F2%29-floor%28y%2F2%29+%3D+c%2C+x%2Bfloor%28%28y%2B1%29%2F2%29+%3D+r%29+where+x%3D+0+and+y+%3D+2+and+h%3D5
i take the results of that, and plug in c and r into the equation to get the x/y:
http://www.wolframalpha.com/input/?i=%28x%2Bfloor%28h%2F2%29-floor%28y%2F2%29+%3D+c%2C+x%2Bfloor%28%28y%2B1%29%2F2%29+%3D+r%29+where+c%3D+1+and+r+%3D+1+and+h%3D5
wolfam is able to get the correct result in the integer solution panel, but i don't know how it got that result.
first of all, I am working on an isometric game, and align my tile's are layed out like so:
so, here's the problem:
the numbers are arranged in how the tile's are layed out in memory, however, i want to be able to get a patch of tile's relative to how the white lines are layed out.
for example: column 1 is 6, 9, and 13. 2 is 3, 7, and 10, and 3 is 1, 4, and 8.
so my input would be something like this: the bottom tile's index in the world(in this case that is tile #6), and then i'd specify which tile i was last on, and finally i'd pass the column and row size to get the chunk of.
the goal is to quickly determine which column/row the last tile is on, increment first by column, then by row. so i'd iterate over tiles 6, 9, 13, 3, 7, 10, 1, 4, and 8.
so, I've figured out how to specify a tile index, and get it's column/row with the following formula:
Code:
//above example, the width and height can be taken as 3, and 5.
//note all divisions are integers, and round down.
void Get(int Index){
int x = Index%width;
int y = floor(Index/width);
int column = x+floor(height/2-((height&1)^1))-floor(y/2);
int row = x+floor((y+1)/2);
}however, i also need to be able to input the column/row and get the tile index(or at least the x/y).
this is the math I've tried to do, but it's obviously not correct:
Code:
int x = Index%width;
int y = Index/width;
int column = x+(height/2-((height&1)^1))-(y/2);
int row = x+(y+1)/2;
width = 3, height = 5 = (5/2 = 2 as int)
Index(x, y) = column, row
Index: 0 (0, 0) = 2, 0
c = x+2-y/2;
2 = x+2-y/2
-2 = -2
0 = x-y/2
+y/2 =+y/2
y/2 = x
*2 = *2
y = 2x
r = x+(y+1)/2
0 = x+(2x+1)/2
0 = x+x ?//not sure if my math here is correct, as it's integer math(or you can think of it as all divisions are rounded down), the 1/2 would round out right?
0 = 2x
/2 = /2
0 = x
y = 2x = 2(0) = 0
Index: 3(0, 1) = 2, 1
c = x+2-y/2
2 = x+2-y/2
-2 = -2
0 = x-y/2
+y/2 = +y/2
y/2 = x
*2 = *2
y = 2x
r = x+(y+1)/2
1 = x+(2x+1)/2
1 = x+x ?
1 = 2x
/2 = /2
0 = x
y = 2x = 2(0) = 0 != 1as you can see that doesn't work. however, after inputing the equations into wolfam:
http://www.wolframalpha.com/input/?i=%28x%2Bfloor%28h%2F2%29-floor%28y%2F2%29+%3D+c%2C+x%2Bfloor%28%28y%2B1%29%2F2%29+%3D+r%29+where+x%3D+0+and+y+%3D+2+and+h%3D5
i take the results of that, and plug in c and r into the equation to get the x/y:
http://www.wolframalpha.com/input/?i=%28x%2Bfloor%28h%2F2%29-floor%28y%2F2%29+%3D+c%2C+x%2Bfloor%28%28y%2B1%29%2F2%29+%3D+r%29+where+c%3D+1+and+r+%3D+1+and+h%3D5
wolfam is able to get the correct result in the integer solution panel, but i don't know how it got that result.