The
spacetime diagram is really the best way to understand what is going on.
Here are two [related] explanations of the
symmetry of time-dilation
with spacetime diagrams (with likely more detail that you may want).
EXPLANATION #1:
based on my Insight
https://www.physicsforums.com/insights/spacetime-diagrams-light-clocks/
and my paper "Relativity on Rotated Graph Paper" [published:
http://aapt.scitation.org/doi/10.1119/1.4943251 , draft:
https://arxiv.org/abs/1111.7254 ]
(Read that Insight to learn HOW I constructed these diagrams in this section.)
Note: Here, my t axis is vertical... as in my relativity books.
These are spacetime-diagrams of the light-signals in the light-clocks of Alice and Bob (where Bob has velocity (3/5)c in this frame.)
The reflection events M and N are simultaneous according to Alice [at rest in this frame], and this occurs at time (1/2)tick according to Alice.
Alice's first tick is at T.
The reflection events Y and Z are simultaneous according to Bob [in motion in this frame], and this occurs at time (1/2)tick according to Bob.
Bob's first tick is at F.
At T, draw a line parallel to MN
[...this turns out to be tangent to the unit hyperbola]
and notice how that line intersects Bob's worldline OF before event F.
So, Alice says that Bob's clock takes longer to tick that her own.
At F, draw a line parallel to YZ
[...this turns out to be tangent to the same unit hyperbola]
and notice how that line intersects Alice's worldline OT before event T.
So, Bob says that Alice's clock takes longer to tick that his own.
To make things easier to see, we can string up a bunch of clock-ticks for each observer... now we can count.
(from my paper)
The time-dilation factor according to Alice is OP/OQ=5/4.. she says when her 5 ticks elapse, only 4 have elasped for Bob.
The time-dilation factor according to Bob is OP'/OQ'=5/4.. he says when his 5 ticks elapse, only 4 have elasped for Alice.
EXPLANATION #2:
(It's the same argument... but using the hyperbola
["what plays the role of the unit circle in Special Relativity"] more explicitly
... and you can play the simulation (and extract numbers is you wish).)
https://www.desmos.com/calculator/ti58l2sair
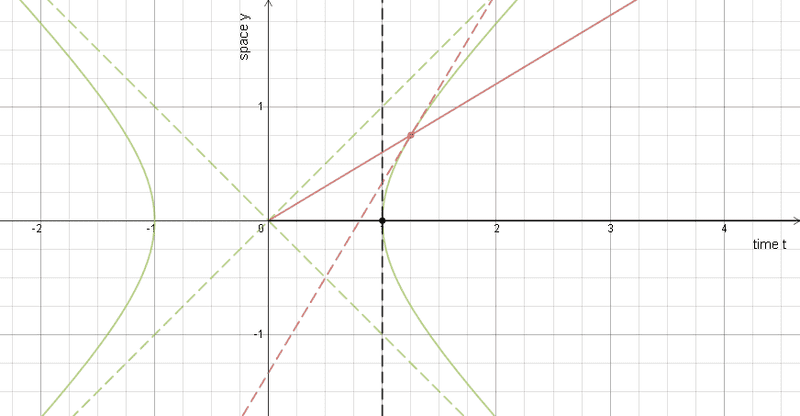
Note: Here, my t axis is horizontal... like the usual position-vs-time graph.
The green dashed-line is the light-cone for the event at the origin of the diagram (call that event O).
The forward hyperbola represents one tick after that origin event for all inertial observers that meet at event O.
One observer has a solid black worldline and is at rest in this frame, and
the other has a solid red worldline who is moving with velocity (3/5)c in this frame.
Their intersections with the hyperbola identify tangent-lines (drawn as black and red dashed lines) to the hyperbola which represent lines of simultaneity for that observer.
Note the symmetry:
- The black dashed-line of simultaneity intersects the red worldline before the red worldline intersects the hyperbola...
in fact, at 4/5 of what could be called the red radius vector.
According to the black observer, it takes 5/4 longer for the red observer's clock to tick compared to his own.
- The red dashed-line of simultaneity intersects the black worldline before the black worldline intersects the hyperbola...
in fact, at 4/5 of what could be called the black radius vector.
According to the red observer, it takes 5/4 longer for the black observer's clock to tick compared to his own.
This factor of 5/4 is the
time-dilation factor ##\gamma## for a relative-velocity of ##v=(3/5)c##.
(In the Desmos simulation, you can find the time-dilation factor by seeing where that observer's line of simultaneity intersects the horizontal t-axis.
Click on that intersection... For the red dashed-line, it gives (0.8,0). The time-dilation factor for the red observer 1/0.8=5/4 in this frame. For black, the time-dilation factor is 1/1.0=1 since the black observer happens to be at rest in this frame.
(optional...)
You can use the sliders to modify their velocities. For general situations, you have to compare the ratios along the other worldline.
For example,
[sorry for the not-so-pleasant numbers]
The relative-velocity for ##v_1=4/10## and ##v_2=-3/10## is ##v_r=\frac{v_1-v_2}{1-v_1v_2}=5/8##,
which leads to a ##\gamma=\frac{1}{\sqrt{1-v_r^2}}=8/\sqrt{39}\approx 1.281##.
That is equal to the ratio 1.0911/0.8517 [using the t-components] or ##\frac{\sqrt{1.0911^2+.4364^2}}{\sqrt{8517^2+.3407^2}}## [using the pythagorean theorem... since the ratio of segments on the same line is an affine invariant.]... and similarly for the other worldline.
Time-dilation goes away if you move the slider to E=0 (Galilean physics).
You get
@Ibix 's argument if you move the slider to E= -1 (Euclidean geometry).