- #1
f8pc
- 11
- 0
Is there any way to prove that speeding up before a hill in a car will save you gas compared to maintaining your speed on the hill?
Here is the situation:
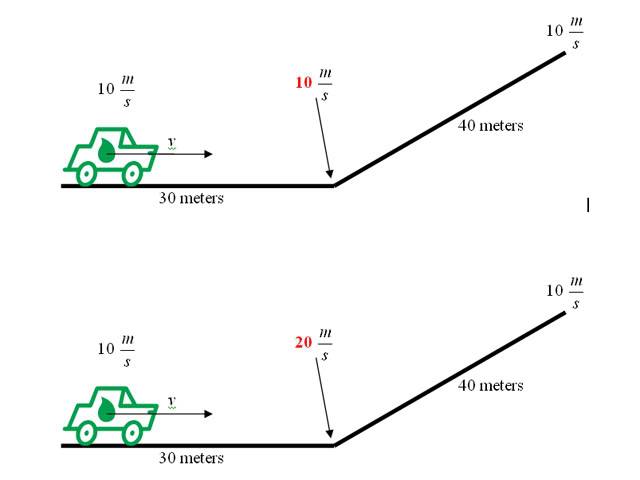
Notice, the one car maintains 10m/s throughout while the second car accelerates to 20m/s on the flat part. Both cars will have the same potential and kinetic energy at the end.
My original approach was to convert MPG of my car (35 mi/gal) to J/m (aka Netwons) by using the conversion factor of 34.8 x 10^6 J/L, which I did and got 2338.95 Netwons of force. Since MPG is presumably measured on a flat surface with a constant speed, that means my car requires 2338.95 Netwons of force to maintain speed so the force of friction is also 2338.95 N. Therefore, since I had the force of friction total of the internal parts of my car, I thought the rest of the problem would be easy. However, when I did all the math, the result showed that the energy required was the same, but that goes against the saying that you should speed up before hills--is that unfounded?
Thanks for any help and if you need any clarification, I'd be willing to explain anything. This really interests me so I'd love to know what you guys think.
-Paul
Here is the situation:
Notice, the one car maintains 10m/s throughout while the second car accelerates to 20m/s on the flat part. Both cars will have the same potential and kinetic energy at the end.
My original approach was to convert MPG of my car (35 mi/gal) to J/m (aka Netwons) by using the conversion factor of 34.8 x 10^6 J/L, which I did and got 2338.95 Netwons of force. Since MPG is presumably measured on a flat surface with a constant speed, that means my car requires 2338.95 Netwons of force to maintain speed so the force of friction is also 2338.95 N. Therefore, since I had the force of friction total of the internal parts of my car, I thought the rest of the problem would be easy. However, when I did all the math, the result showed that the energy required was the same, but that goes against the saying that you should speed up before hills--is that unfounded?
Thanks for any help and if you need any clarification, I'd be willing to explain anything. This really interests me so I'd love to know what you guys think.
-Paul