Spinning Bike Wheel Example, how is angular momentum conserved?

[alkaspeltzar]

In the classic example of a person holding a spinning bike wheel, as they flip the wheel over, angular momentum is conserved by the person/chair spinning with 2x the angular momentum of the initial wheel. Not questioning that.

However, I thought ang momentum is always conserved about a point/axis? IF so, how do they add since the wheel and person are about two different axis?

See below, you can see they add, but are showing the angular momentum of the wheel adding to the angular mom. of the chair/person, which are two different axis.

IS it because the ang momentum of the wheel prior to flipping is the same at any axis? Looking for clarification on why they can add.

 

[kuruman]

They add although they are about different axes because the center of mass of the wheel does not move relative to the stool axis. If it did, then yes, you would have to consider the "orbital" angular momentum of the wheel.

 

[alkaspeltzar]

They add although they are about different axes because the center of mass of the wheel does not move relative to the stool axis. If it did, then yes, you would have to consider the "orbital" angular momentum of the wheel.

I understand oribtal Ang momentum, but I don't see the difference. Isn't the wheel still rotating around the stool axis?

The wheel doesn't move relative to the person or stool, is that what you mean?

 

[kuruman]

Yes, sorry, I was a bit hasty with my explanation. The angular momentum vector that points up in the "final" picture is the vector sum of the spin of the person plus chair, the spin of the wheel and the orbital angular momentum of the spinning wheel. Strictly speaking, there should be three vectors drawn in the "final" picture, two of which are up and have a combined magnitude of twice the magnitude of the down vector.

 

[alkaspeltzar]

Yes, sorry, I was a bit hasty with my explanation. The angular momentum vector that points up in the "final" picture is the vector sum of the spin of the person plus chair, the spin of the wheel and the orbital angular momentum of the spinning wheel. Strictly speaking, there should be three vectors drawn in the "final" picture, two of which are up and have a combined magnitude of twice the magnitude of the down vector.

Okay so originally there is the angular momentum of the wheel, and since it is not moving to the axis of the chair, it would be equal to the Ang momentum of the wheel about the chairs axis. Like you said, if the cofm doesn't move, axis doesn't matter

But then as you flip the wheel, there would be a negative angular momentum of the wheel. This would cause then the angular momentum of the whole chair/person which includes the oribital portion of the wheel. This is twice the Ang momentum, so the sum of it all is still the same as inital.

Does my interpretation make sense? Thks for help

 

[A.T.]

However, I thought ang momentum is always conserved about a point/axis? IF so, how do they add since the wheel and person are about two different axis?

Note that L_b contains the angular momentum from the disc translating along a circle around the stool axis. See:
https://en.wikipedia.org/wiki/Parallel_axis_theorem

 

[alkaspeltzar]

Note that L_b contains the angular momentum from the disc translating along a circle around the stool axis. See:
https://en.wikipedia.org/wiki/Parallel_axis_theorem

That's what I was saying in my above explanation. If you take the angular momentum of the disk spinning about its axis or the chair aixs, it is the same. This is because the translation part is part of the entire chair/disk/person rotation. Thks for clarifying

 

[Andrew Mason]

Summary:: Ang momentum of the wheel is about a different axis than the person/chair, how can they be added together?

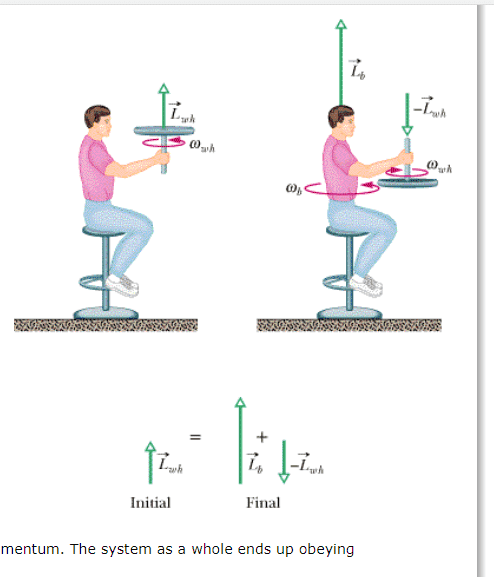
In the classic example of a person holding a spinning bike wheel, as they flip the wheel over, angular momentum is conserved by the person/chair spinning with 2x the angular momentum of the initial wheel. Not questioning that.

However, I thought ang momentum is always conserved about a point/axis? IF so, how do they add since the wheel and person are about two different axis?

See below, you can see they add, but are showing the angular momentum of the wheel adding to the angular mom. of the chair/person, which are two different axis.

IS it because the ang momentum of the wheel prior to flipping is the same at any axis? Looking for clarification on why they can add.

Good question. It is not immediately obvious that you can simply add angular momentum vectors.
One has to work it out.

If we take a point mass with mass m relative to an inertial point c, its angular momentum is:
L = r x mv = r x m(dr/dt) where r is the displacement vector from c to m.

If we measure the angular momentum relative to c at an arbitrary inertial point p (same inertial frame) such that the displacement vector from p to c is s, (the displacement from p to m being s + r) we get:
L' = r x m(d(s + r)/dt) = r x m(ds/dt) + r x m(dr/dt) = r x m(dr/dt) = L [since ds/dt = 0]

It is a bit more math but it can similarly be shown that if p is a point in any inertial frame, moving at velocity vp relative to c, L' = L

So the angular momentum of a point mass relative to an inertial point c is the same vector (same magnitude and direction) at all inertial points (ie. it is the same regardless of the inertial point at which it is measured).

So to determine the total angular momentum of a system of two point particles m and m' about two different inertial points c and c' (respectively), measuring their angular momentum at an arbitrary inertial point in the same inertial reference frame can be achieved by simply add their angular momentum vectors as measured at c and c'. Angular momentum is, therefore, an intrinsic property of the point mass.

Generalizing to n point particles in a rigid body, we can see that the angular momentum of a rigid body about an axis can be determined by simply adding the angular momenta of each point mass that comprises the body about a point on the axis.

Generalizing further and taking n rigid bodies comprising a system, we can say that the angular momentum of the system is the sum of the angular momenta vectors of each body.

Since dL/dt = r x F = τ the angular momentum of a rigid body rotating about an axis can only change if there is a torque applied that is external to the point mass or rotating body.

We then configure two freely rotating bodies together in a system on which no external torque is applied:
L = L1 + L2. Because there is no external torque, this means that dL/dt = dL1/dt + dL2/dt = 0. The angular momenta of each of those two bodies can change because one body can apply a torque to the other. But we can see that dL1/dt = - dL2/dt so there must be an equal and opposite torque applied by the other. We can, therefore, conclude that the sum of the angular momenta vectors of each body in the system is conserved in the absence of an external torque.

I hope that clarifies more than it confuses.

AM

 

[kuruman]

Good question. It is not immediately obvious that you can simply add angular momentum vectors.
One has to work it out.

The person + stool + wheel system is only partially isolated in the sense that the floor can exert torques only in the horizontal direction which implies that the vertical component of the system's angular momentum must be conserved. In other words, the sum of all the "before" vertical angular momenta must be equal to the sum of all the "after" vertical angular momenta. If the person initially holds the wheel with its axis horizontal and turns it by 90^o to put it along the vertical, the stool's spin will be opposite to the wheel's to keep the total vertical angular momentum zero. I used to spin myself my self this way, stop and then spin the other way when I did the demo during my teaching days.

This situation is the rotational equivalent of the two skaters moving together and then pushing against each other. Regardless of the direction of the action-reaction push, linear momentum in the horizontal direction is conserved because the ice can exert forces only in the vertical direction.

 

[Andrew Mason]

In the system as described, turning the wheel axis is going to exert a torque with a horizontal component. Since the stool can only turn on a vertical axis, that horizontal change in angular momentum is applied to the earth. So, as you point out, only angular momentum in the vertical direction will be conserved. This problem can be avoided if the system was gimballed so that no axis is constrained.

AM