- #1
arivero
Gold Member
- 3,430
- 140
- TL;DR Summary
- links and general commentary
Confronted with my inability to grasp Witten's Susy QM examples of supersymmetry breaking, I concluded that the problem was that I was not understanding spontaneous symmetry breaking in simpler contexts.
It seems that SSB is not possible in QM because of tunneling between the different states, and that it becomes possible in QFT because the transition probability becomes zero in infinite volume, albeit almost no textbook takes the time to prove it, just state it -or not-.
The best question I have found is this one in PhysicsExchange, and it links to an interesting paper couple of papers by Landsman
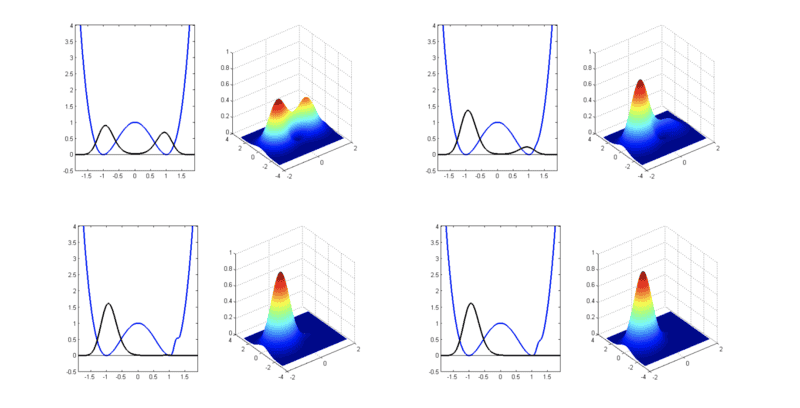
calculating the flea, they say in the cat instead of the elephant It also links to a preprint by Thirring and Narnhofer, that mentions the case of SUSY QM.
It also links to a preprint by Thirring and Narnhofer, that mentions the case of SUSY QM.
The double (and multiple) well symmetry breaking in QM was taken with great interest in the eighties, I guess the sparks were Witten's Susy QM, Coleman instantons, and the analysis of Jona-Lasinio, Martinelli and Scoppola, as well as Barry Simon's "flea in the elephant" for analysts. It was revisited periodically each time a generation finished their formative years. I see a revisit by M-K in 1992, by myself in 1994 (uploaded later), Casahorran in 2001 (triple well) or Alhendi-Lashin in 2004. Related topics as transparent or shape invariant potentials and delta potentials are also revisited frequently. Still I do not find a consistently complete approach to the topic, including things as Witten's spontaneous susy breaking, where the partner has been fully collapsed out and is not a normalised state anymore, or the impossibility of an analogous of Goldstone theorem for localization.
It seems that SSB is not possible in QM because of tunneling between the different states, and that it becomes possible in QFT because the transition probability becomes zero in infinite volume, albeit almost no textbook takes the time to prove it, just state it -or not-.
The best question I have found is this one in PhysicsExchange, and it links to an interesting paper couple of papers by Landsman
calculating the flea, they say in the cat instead of the elephant
The double (and multiple) well symmetry breaking in QM was taken with great interest in the eighties, I guess the sparks were Witten's Susy QM, Coleman instantons, and the analysis of Jona-Lasinio, Martinelli and Scoppola, as well as Barry Simon's "flea in the elephant" for analysts. It was revisited periodically each time a generation finished their formative years. I see a revisit by M-K in 1992, by myself in 1994 (uploaded later), Casahorran in 2001 (triple well) or Alhendi-Lashin in 2004. Related topics as transparent or shape invariant potentials and delta potentials are also revisited frequently. Still I do not find a consistently complete approach to the topic, including things as Witten's spontaneous susy breaking, where the partner has been fully collapsed out and is not a normalised state anymore, or the impossibility of an analogous of Goldstone theorem for localization.