Spring-mass system, two carts, two springs

[SithsNGiggles]

Homework Statement

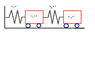
Take the example in Figure 3.12 on pg 117 (see attachment) with parameters $m_1=m_2=1$ and $k_1=k_2=1$. Does there exist a set of initial conditions for which the first cart moves but the second cart does not? If so, find those conditions.

Homework Equations

The Attempt at a Solution

Here's my set-up:
$\begin{cases} x_1'' = -2x_1+x_2\\ x_2'' = x_1-x_2 \end{cases}$

And I'm not sure whether my reasoning is valid here, but since we're trying to find conditions for which $m_2$ doesn't move, does that mean $x_2=0$?

This would leave me with just
$x_1''=-2x_1$,
and from the second equation we get $x_1=0$ as well.

Because of this, I'm led to believe the initial conditions are something like $x_1(0)=0$ and $x_2(0)=0$.

 

[BruceW]

I don't think your reasoning is correct. If someone told you that object 2 doesn't move, then what would you say about X'₂ and X''₂ ? This is the line of reasoning you should go down.

 

[SithsNGiggles]

What about this: If the second cart doesn't move, that means $x_2=0$, right? Which in turn means that $x'_2=0$ and $x''_2=0$. Plugging these into the system yields $x_1=0$, which means the first cart also doesn't move. Thus, there are no initial conditions that will allow this situation to occur, unless the second cart was held down against the surface.

 

[BruceW]

What about this: If the second cart doesn't move, that means $x_2=0$, right?

Well, you've guessed the answer, but you have not got any reason to say why X₂ is zero. Try doing it the other way around. We are told to find out what motion is possible if X₂ is constant. So for now, don't assume X₂ is zero. Just assume that it is constant. OK, so what does this tell us about the twice derivative of X₂ ?