Spring potential energy comparison

AI Thread Summary
The discussion centers on comparing the potential energy of a spring at two different positions, A and B, after being stretched. The potential energy is calculated using the formula PE = 1/2 kx^2, where 'x' represents the distance the spring is stretched. It is noted that if the spring is stretched to double the distance at position B compared to position A, the potential energy at B will be four times greater due to the x^2 relationship in the equation. Participants are encouraged to clarify the problem statement and provide their reasoning for the solution. Understanding the implications of the spring's stretch distance is crucial for solving the problem accurately.
tourniquet63
Messages
3
Reaction score
0

Homework Statement



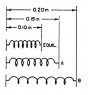
A 0.10 m spring is stretched from equilibrium position to position A and then to position B as shown in the diagram below. Compared to the spring’s potential energy at A, what is its potential energy at B?

Homework Equations



PE = 1/2 kx^2

The Attempt at a Solution



Having trouble with this one. Is it twice as much or four times as much?
 

Attachments

  • spring.png
    spring.png
    5.8 KB · Views: 433
Last edited:
Physics news on Phys.org
Please retype the problem statement, the question is missing.
Please fill in section 2 also.
And state or show how you arrived at your answer.

Thanks, and welcome to these forums!
 
Ooops! thanks
 
In your relevant equation, what is the description of 'x'...what distance is it describing?
 
x is the distance the spring is compressed or stretched
 
tourniquet63 said:
x is the distance the spring is compressed or stretched
Ok so in the first part it is stretched a certain distance and in the second part it is stretched double that distance. Since the PE equation includes an x^2 term, if x doubles then the PE must be ___?___ times greater.
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Pan suspended by a spring (Energy + SHM)
Replies
20
Views
3K
Irodov- 1.123- Simple conceptual question with two masses connected by a spring
Replies
20
Views
564
Calculating the Energy Absorbed by a Spring in a Car Suspension System
Replies
5
Views
2K
Why can we move the spring with constant speed when we apply a force?
Replies
29
Views
2K
Find elastic energy in the compressed spring.
Replies
12
Views
3K
Question about springs and rotational/translational energy
Replies
4
Views
1K
Distribution of Energy when work is done on a system of 2 masses connected by a spring
Replies
17
Views
1K
Initial velocity of bird landing on horizontal wire modeled as spring
Replies
7
Views
918
A rocket on a spring, related to potential/kinetic energy
Replies
3
Views
2K
Time period of SHM & Energy conservation in pulley-spring-block system
Replies
24
Views
3K

Hot Threads

Recent Insights

Back
Top