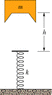dorkymichelle
- 40
- 0
Homework Statement
A block of mass m = 3.5 kg is dropped from height h = 81 cm onto a spring of spring constant k = 2220 N/m (Fig. 8-37). Find the maximum distance the spring is compressed.
Homework Equations
Pe(spring) = 1/2kx2
Pe(gravity)=mgh
Ke = 1/2mv2
The Attempt at a Solution
so far, i got mgh+1/2mvi2 =1/2mvf2 = 1/2kx2
because the energy used to compress the spring is the amount of energy from the end of the drop.
but I don't have initial velocity or final velocity. or can i use 0 as final velocity at the point that the object hits the spring..