Static equilibrium | Uniform sphere on incline | Determining friction

[I_Try_Math]

Homework Statement

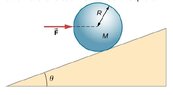
A horizontal force $\vec{F}$ is applied to a uniform sphere in direction exact toward the center of the sphere, as shown below. Find the magnitude of this force so that the sphere remains in static equilibrium. What is the frictional force of the incline on the sphere?

Relevant Equations

$\sum{\tau} = 0$
$\sum{F} = 0$

So if I understand correctly the forces acting on the sphere are $\vec{F}$, the normal force, friction, and the weight of the sphere. In order for the conditions of static equilibrium to be met the net torque must be zero.

The torque about the center of the sphere created by the normal force, the weight force, and $\vec{F}$ are all zero because the angle between their position vectors and themselves are zero (rFsin0 = 0). The only other force is friction which acts along the incline. So if friction is nonzero, then net torque is nonzero which contradicts the premises of the question?

Any help is appreciated.

 

[Orodruin]

So if friction is nonzero, then net torque is nonzero which contradicts the premises of the question?

.. and therefore the conclusion must be …

 

[I_Try_Math]

.. and therefore the conclusion must be …

That there is no friction I suppose. To me the question's wording seems to imply that there's nonzero friction but I guess not.

 

[kuruman]

That there is no friction I suppose. To me the question's wording seems to imply that there's nonzero friction but I guess not.

The question does imply that. However, just like the normal force, static friction adjusts itself to provide the observed acceleration.

Say force $\mathbf F$ is applied to the sphere with a horizontal rod and the contact between rod and sphere has coefficient of static friction $\mu_s.$ If friction is not needed to provide zero acceleration, then the specific value of $\mu_s$ is irrelevant; the answer is the same.

Your solution is incomplete. You have shown that the sphere can be in rotational equilibrium when the friction is zero. This does not necessarily mean that the sphere is also in translational equilibrium. How do you know that, with zero friction, the sum of the forces can be zero? In other words, show that there is a value of the normal force such that the net force on the sphere is zero.

 

[erobz]

That there is no friction I suppose. To me the question's wording seems to imply that there's nonzero friction but I guess not.

There is something I could use some convincing on...make the angle $\theta = \frac{\pi}{2}$, this seems problematic without friction, and it also seems problematic with friction at the same time? It seems to be that it can only be achieved if there is a vertical frictional force at the point of application of $F$?

 

[kuruman]

There is something I could use some convincing on...make the angle $\theta = \frac{\pi}{2}$, this seems problematic without friction, and it also seems problematic with friction at the same time? It seems to be that it can only be achieved if there is a vertical frictional force at the point of application of $F$?

There are two "fixed" forces with respect to $\theta$ acting on the sphere, the vertical weight $\mathbf W$ and the horizontal force $\mathbf F$. If we exclude friction, then the normal force must be equal to the vector sum of the two fixed forces in order to have equilibrium, $$\mathbf N=\mathbf W+\mathbf F.$$ This condition can be satisfied as long as the normal force is not collinear with $\mathbf F.$ It breaks down at $\theta=\frac{\pi}{2}.$

However this 90° rotation would work (gravity is still from the top of the screen to the bottom.)

 

[erobz]

There are two "fixed" forces with respect to $\theta$ acting on the sphere, the vertical weight $\mathbf W$ and the horizontal force $\mathbf F$. If we exclude friction, then the normal force must be equal to the vector sum of the two fixed forces in order to have equilibrium, $$\mathbf N=\mathbf W+\mathbf F.$$ This condition can be satisfied as long as the normal force is not collinear with $\mathbf F.$ It breaks down at $\theta=\frac{\pi}{2}.$

There is something very unsatisfying about it failing precisely at $\frac{\pi}{2}$. We do the "push box on the vertical wall problem" regularly, friction is the objective reality there. Now, replace the box with a sphere and it goes to hell in a hand basket...

 

[kuruman]

There is something very unsatisfying about it failing precisely at $\frac{\pi}{2}$. We do the "push box on the vertical wall problem" regularly, friction is the objective reality there. Now, replace the box with a sphere and it goes to hell in a hand basket...

I don't see it that way. You start with two forces, one horizontal $\mathbf F$ and one vertical $\mathbf W.$ As long as the normal force can have a horizontal component to match $\mathbf F$ and a vertical component to match $\mathbf W$, there can be equilibrium with zero friction.

This condition cannot be met precisely at $\theta = 0$ at which $\mathbf N$ cannot have a horizontal component and at $\theta = \frac{\pi}{2}$ at which $\mathbf N$ cannot have a vertical component. Any other angle between the two extreme values works with zero friction.

At the specific value $\theta = 0$, if there is no friction, the sphere will slide to the right with acceleration $a=F/m.$ At the specific value $\theta = \frac{\pi}{2}$, if there is no friction, the sphere will slide straight down $a=g.$

At the specific value $\theta = 0$, if there is friction, the sphere will slide to the right with acceleration $a=F/m.$ If there is friction, and $F<\mu_s mg$, the sphere will roll without sliding to the right with acceleration $a_{cm}=\frac{5}{7}(F/m)$. This requires $f_s=(2/7)F$ to the left.

At the specific value $\theta = \frac{\pi}{2}$, if there is no friction, the sphere will slide straight down $a=g.$ To have equilibrium if there is friction, an additional assumption needs to be made that force $\mathbf F$ is applied with, say, a horizontal rod and that the contact is "rough". Then, as long as the relevant coefficients of static friction are high enough to have no slipping, at the points of contact with the rod and the wall the upward forces of friction are equal (this balances the torques about the center) with a value of $\frac{1}{2}mg$ each to balance the weight. The horizontal force is balanced by the normal force. Nothing goes to hell in a hand basket.

(Edited for typos.)

 

[Lnewqban]

That there is no friction I suppose. To me the question's wording seems to imply that there's nonzero friction, but I guess not.

If we replace F with a vertical wall, we are creating a geometrical restriction (two converging planes) for the sphere to move or rotate under the action of its own weight.

Friction force is always a natural reaction to imminent of fully developed movement.
No relative movement sphere-wall-incline = No friction forces

 

[erobz]

I don't see it that way. You start with two forces, one horizontal $\mathbf F$ and one vertical $\mathbf W.$ As long as the normal force can have a horizontal component to match $\mathbf F$ and a vertical component to match $\mathbf W$, there can be equilibrium with zero friction.

This condition cannot be met precisely at $\theta = 0$ at which $\mathbf N$ cannot have a horizontal component and at $\theta = \frac{\pi}{2}$ at which $\mathbf N$ cannot have a vertical component. Any other angle between the two extreme values works with zero friction.

At the specific value $\theta = 0$, if there is no friction, the sphere will slide to the right with acceleration $a=F/m.$ At the specific value $\theta = \frac{\pi}{2}$, if there is no friction, the sphere will slide straight down $a=g.$

At the specific value $\theta = 0$, if there is friction, the sphere will slide to the right with acceleration $a=F/m.$ If there is friction, and $F<\mu_s mg$, the sphere will roll without sliding to the right with acceleration $a_{cm}=\frac{5}{7}(F/m)$. This requires $f_s=(2/7)F$ to the left.

At the specific value $\theta = \frac{\pi}{2}$, if there is no friction, the sphere will slide straight down $a=g.$ To have equilibrium if there is friction, an additional assumption needs to be made that force $\mathbf F$ is applied with, say, a horizontal rod and that the contact is "rough". Then, as long as the relevant coefficients of static friction are high enough to have no slipping, at the points of contact with the rod and the wall the upward forces of friction are equal (this balances the torques about the center) with a value of $\frac{1}{2}mg$ each to balance the weight. The horizontal force is balanced by the normal force. Nothing goes to hell in a hand basket.

(Edited for typos.)

I would say there is no equilibrium at $\theta =0$ with or without friction. At the extreme of the vertical wall there needs to suddenly be friction at the center of gravity as a minimal model, or friction at point of application of $F$ and the wall to be in static equilibrium.

It bothers me as inconsistent. The limits of the model are not harmonious with the stuff in between. Surely it’s worth a mention as we are always instructed to “check the limits” to see if the model makes sense. To me it’s a gap( infinitesimal as it may be)that is not explained away with ease, maybe not at all. So I guess I would respectfully disagree…the discontinuity is still fishy.

 

[haruspex]

It bothers me as inconsistent.

As the angle steepens, a smaller fraction of the normal force is available to counter the weight. So the normal force increases, requiring a greater F to balance its horizontal component. In the limit $\theta\rightarrow\pi/2$, those horizontal forces $\rightarrow\infty$.
I don’t see that as a sudden inconsistency.

 

[kuruman]

Surely it’s worth a mention as we are always instructed to “check the limits” to see if the model makes sense.

OK, let's check the limits. Look at the FBD on the right. From the right triangle obtained by adding the three forces, the equilibrium relation of magnitudes is $$\tan\theta=\frac{F}{W}~~~(N=\sqrt{F^2+W^2}.)$$
When $\theta=0$, ($\tan\theta=0$), we must have $F=0$. That makes sense and is consistent with $~\mathbf F_{\text{net}}=m\mathbf a~$. In the vertical direction $\mathbf N=-\mathbf W$. Unless $F=0$, there cannot be equilibrium because $\mathbf F$ is the only horizontal force.

When $\theta=\frac{\pi}{2}$,($\tan\theta=\infty$), we must have $W=0$. This, too, makes sense and we can apply similar reasoning as before but with the directions swapped. Here, the normal force becomes horizontal and can easily balance the pushing force, $\mathbf N=-\mathbf F.$ Unless $W=0$, there cannot be equilibrium because $\mathbf W$ is the only vertical force.

 

[jbriggs444]

Friction force is always a natural reaction to imminent of fully developed movement.
No relative movement sphere-wall-incline = No friction forces

View attachment 356354

The depicted situation (inclined floor and vertical wall) is statically indeterminate. The frictional forces can consistently take on a range of values.

In the real world, the finite elasticity of materials and the manner in which the construct is assembled may (or may not) determine the resulting frictional forces.

 

[haruspex]

No relative movement sphere-wall-incline = No friction forces

I think you mean that if there would be no movement in the absence of friction then there are no frictional forces. But as @jbriggs444 points out, that is not necessarily true either.

 

[Lnewqban]

I think you mean that if there would be no movement in the absence of friction then there are no frictional forces. But as @jbriggs444 points out, that is not necessarily true either.

Sorry, I don't follow.

 

[jbriggs444]

Sorry, I don't follow.

The fact that an equilibrium can be attained without the presence of friction does not preclude the possibility of an equilibrium with the presence of friction.

Consider, for example, the case of a splitting wedge or piton. The wedge can be in there tight. Or it can be in there loose.

 

[erobz]

View attachment 356361OK, let's check the limits. Look at the FBD on the right. From the right triangle obtained by adding the three forces, the equilibrium relation of magnitudes is $$\tan\theta=\frac{F}{W}~~~(N=\sqrt{F^2+W^2}.)$$
When $\theta=0$, ($\tan\theta=0$), we must have $F=0$. That makes sense and is consistent with $~\mathbf F_{\text{net}}=m\mathbf a~$. In the vertical direction $\mathbf N=-\mathbf W$. Unless $F=0$, there cannot be equilibrium because $\mathbf F$ is the only horizontal force.

When $\theta=\frac{\pi}{2}$,($\tan\theta=\infty$), we must have $W=0$. This, too, makes sense and we can apply similar reasoning as before but with the directions swapped. Here, the normal force becomes horizontal and can easily balance the pushing force, $\mathbf N=-\mathbf F.$ Unless $W=0$, there cannot be equilibrium because $\mathbf W$ is the only vertical force.

I'm not deniying any of that (I belive). This is what I'm trying to get across as fishy:

The one on the right has a solution for $F$ that is finite. The diagram on the left does not. This model of "no required friction" would seem to do poorly at some point.

It's not just friction appearing at the wall-ball interface that resolves this because there would still be a net torque unchallenged. At a minimum it requires both friction and deformation, such that the normal force can be offset (countering the torque from the weight at the wall) that an equilibrium can exist.

 

[kuruman]

I'm not deniying any of that (I belive). This is what I'm trying to get across as fishy:

View attachment 356371

The one on the right has a solution for $F$ that is finite. The diagram on the left does not. This model of "no required friction" would seem to do poorly at some point.

I am sorry, I don't get what you are trying to get across. If the arrows represent forces, neither situation can be in equilibrium because when you add two orthogonal non-zero vectors you cannot get a sum of zero.

 

[erobz]

I am sorry, I don't get what you are trying to get across. If the arrows represent forces, neither situation can be in equilibrium because when you add two orthogonal non-zero vectors you cannot get a sum of zero.

The right side has a finite $F$, look closely at the angle diagram and it should illustrate my point. (The normal forces are not show here for clarity but it really makes no difference). I'm saying that the right side has a solution according to the mathematics, but the left side diagram does not - can you prove me wrong(rhetorical question I hope)? Anything that gives an infinite change from an infinitesimal displacement do you truly believe to be a viable physical model?

 

[kuruman]

The right side has a finite $F$, look closely at the angle diagram and it should illustrate my point. (The normal forces are not show here for clarity but it really makes no difference)

I looked closely and I didn't see any difference in the angle. I added my own perpendicular lines (in red) to your diagram and they look parallel to yours.

I think that writing a few equations will illustrate your point better.

 

[haruspex]

Sorry, I don't follow.

I should have clarified that it depends on the idealisations being used.
Consider a uniform rectangular block lying on two supports placed symmetrically. This can be in equilibrium without friction, but it would also be in equilibrium if the supports are exerting equal and opposite frictional forces.
If we take the block and supports as rigid, there is no way to figure out what those forces might be.
But in the real world, nonzero horizontal forces would imply some tension or compression of the block, which would involve some deformation. Likewise the supports. So if we knew the details of the deformations and the moduli of the materials we could determine all the forces. So the indeterminacy arises from denying ourselves some of the information.

 

[erobz]

I looked closely and I didn't see any difference in the angle. I added my own perpendicular lines (in red) to your diagram and they look parallel to yours.

View attachment 356372
I think that writing a few equations will illustrate your point better.

They are the same image, with the exception that I say the left diagram is a right angle (notice the black symbol in the corner). In the right there is no physical way to determine that it's not 89.999... degrees and yet the is literally an infinite difference in the required forces $F$ to achieve equilibrium in each scenario. This is evident from the mathematics of this model. I guess everyone just thinks I trolling?

 

[haruspex]

They are the same image, with the exception that I say the left diagram is a right angle (notice the black symbol in the corner). In the right there is no physical way to determine that it's not 89.999... degrees and yet the is literally an infinite difference in the required forces $F$ to achieve equilibrium in each scenario. This is evident from the mathematics of this model. I guess everyone just thinks I trolling?

Did you see my post #11?

 

[erobz]

Did you see my post #11?

Yeah, my problem is I think the problem requires (something like)this for a reasonable resolution where we won't find these infinities from infinitesimal deviations ( I don't see how post 11 renders this unnecessary).

The model in the limit as it is now is absurd. It flat out can't work at vertical? Why should I believe its fine everywhere else?

 

[haruspex]

Yeah, my problem is I think the problem requires (something like)this for a reasonable resolution where we won't find these infinities from infinitesimal deviations ( I don't see how post 11 renders this unnecessary).

View attachment 356375

The model in the limit as it is now is absurd. It flat out can't work at vertical? Why should I believe its fine everywhere else?

It's much the same as trying to pull a massive horizontal rope straight. The straighter you require, the higher the tension, without limit.
Do you reject the notion of 1/x being a valid mathematical function just because it excludes x=0?

 

[Orodruin]

I mean, the model - as most models - is an idealization. I don’t see why you would belive an idealized model having a divergence in a particular would necessarily invalidate that model.

@haruspex rope example is accurate. If your rope were infinitely durable you would require infinite force to straighten it. But no real rope can hold an infinite tension. That does not make it a bad model.

 

[erobz]

I mean, the model - as most models - is an idealization. I don’t see why you would belive an idealized model having a divergence in a particular would necessarily invalidate that model.

I can hold a marble on a smooth vertical surface without anywhere near infinite force (quite a small force actually), so it seems pretty clear that a little friction can go a long(and I mean really long) way given the infinities the model predicts.

 

[Orodruin]

I can hold a marble on a smooth vertical surface without anywhere near infinite force (quite a small force actually), so it seems pretty clear that a little friction can go a long(and I mean really long)way.

That’s not a frictionless surface though. The point here is that even if the surface is frictionless there is a possible equilibrium. That there are actual real cases where the model is not applicable is precisely my point. The rope will break before you reach fully horizontal. Minor frictional force (plus the fact that you will never be able to push with a fully horizontal force) break the model here. That doesn’t mean it is not a useful model in other situations. Just that it is not applicable to that particular limit. People still use Newtonian gravity to build bridges even if it is not valid for very dense objects or objects moving close to the speed of light.

 

[erobz]

That’s not a frictionless surface though. The point here is that even if the surface is frictionless there is a possible equilibrium.

Without deformation there is always going to be an unbalanced torque about the point of contact from the spheres weight. So in the absence for deformation, and friction at the point of the applied force what are we to believe, that the sphere is just spinning in place?

 

[Orodruin]

Without deformation there is always going to be an unbalanced torque about the point of contact from the spheres weight.

No this is incorrect in the case of a non-vertical wall. The model is obviously not accurate for a vertical wall.

 

[erobz]

The model is obviously not accurate for a vertical wall.

But then an infinitesimal displacement away from vertical it is?

 

[Orodruin]

But then an infinitesimal displacement away from vertical it is?

Within the model yes. But as I have already stated - repeatedly - it is obvious that the model breaks down well before that. Just as the rope model does before the rope becomes horizontal.

 

[erobz]

Within the model yes. But as I have already stated - repeatedly - it is obvious that the model breaks down well before that. Just as the rope model does before the rope becomes horizontal.

Ok, I wasn't picking up on that. My point was this model has a window of validity, but it isn't obvious where exactly that is with what is exposed to us in manipulatable variables. I feel a "better" model is the alternative to this, which is what I think you (ultimately) believe too.

 

[Orodruin]

My point was this model has a window of validity

But that is exactly what you have been arguing against!

Most if not all models have limited applicability. Divergences often appear if those limits are taken without keeping this in mind.

 

[jbriggs444]

That’s not a frictionless surface though.

Worse, he is inadvertently providing some upward force with his hand in addition to the intended horizontal force.

 

[erobz]

But that is exactly what you have been arguing against!

Most if not all models have limited applicability. Divergences often appear if those limits are taken without keeping this in mind.

To me it feels worse than what I've encountered in the past... infinite forces from infinitesimal deviations seems unsavory. I'm not an academic. I'm still trying to probe my parents to see if Santa Clause is real or not.

Worse, he is inadvertently providing some upward force with his hand in addition to the intended horizontal force.

I'm aware of that too, but I don't think that helps the argument against reducing the amount of idealization, does it?

 

[jbriggs444]

To me it feels worse than what I've encountered in the past... infinite forces from infinitesimal deviations seems unsavory. I'm not an academic. I'm still trying to probe my parents to see if Santa Clause is real or not.

I'm aware of that too, but I don't think that helps the argument against reducing the amount of idealization, does it?

It helps clarify matters. We do not need to model exotic things like deformation and off center contact forces if the reality primarily involves equal vertical support forces on either side.

I am fine with the idealization and the resulting singularity as the wall becomes vertical.

 

[erobz]

It helps clarify matters. We do not need to model exotic things like deformation and off center contact forces if the reality primarily involves equal vertical support forces on either side.

I am fine with the idealization and the resulting singularity as the wall becomes vertical.

Yeah, friction at both contact point works that of the wall and the ball and the friction of the thing applying the force. My point was its like the model is like fine,fine,fine,...adinfinitum. Suddenly friction is necessary at 90.000000000000000... I still want to spit it out, instead of chewing it. Its too philosophical in flavor to be good food IMO.

I get the model breaks well before that, but I suspect if we add a touch more realism the divergence would vanish?

 

[jbriggs444]

I get the model breaks well before that, but I suspect if we add a touch more realism the divergence would vanish?

In reality there is no such thing as a vertical wall. Or an exact angle of the wall. Or even an unambiguous definition of the "wall". There is no point in pushing reality that far.

We work with models that are good enough.

 

[erobz]

There is no point in pushing reality that far.

But that's the whole ball game!

We work with models that are good enough.

Yeah, so long as it is admitted that good enough is mostly fuzzy in this sport, and new stuff can be found in the fuzz that is groundbreaking. I'm not suggesting that here, but to say you guys don't adjust/fine tune is a bit defeatist. Maybe we teach what is "good enough", but I don't think we truly ever except what is good enough.

 

[Orodruin]

But that's the whole ball game!

It most definitely isn’t. The whole ball game is making useful predictions. That includes both accuracy (good enough for the purpose), reliability, and ease of performing the prediction.

 

[Orodruin]

I'm not suggesting that here, but to say you guys don't adjust/fine tune is a bit defeatist. Maybe we teach what is "good enough", but I don't think we truly ever except what is good enough.

I think you are missing the entire point here. This is a post in the introductory homework forum. The point is helping the OP solve the problem within the constraints of the given model. A discussion of what refinements the model could use in particular limits (or even how the model behaves in those limits) is not part of the problem. It might have been in a more advanced setting, but here that discussion is not productive to the OP because the entire purpose is understanding the simplified model, not to consider where it breaks down and why or what possible refinements could be made to resolve the issues.

 

[Lnewqban]

I should have clarified that it depends on the idealisations being used.
....So if we knew the details of the deformations and the moduli of the materials we could determine all the forces. So the indeterminacy arises from denying ourselves some of the information.

Understood.
In agreement with your valid explanation.
Thank you much, @haruspex and @jbriggs444

Therefore, is there a correct response for the last question in the OP?
"What is the frictional force of the incline on the sphere?"

The way I see it, the OP situation could be considered to be equivalent to a perfectly rigid sphere resting on two perfectly rigid rollers (frictionless axes).

The right-side roller would be rigidly anchored to Earth.

The left-side roller (which center is horizontally aligned with the center of the sphere) would be free to slide on a horizontal guide and being pushed to the right by the exact amount of force needed to keep the theta angle (being equivalent to keep the sphere from rolling or sliding up or down the incline in the OP diagram).

The sphere can be in static equilibrium only for one unique value of force F, just like an airplane remains in horizontal flight only for one value of lift force.

 

[haruspex]

is there a correct response for the last question in the OP?

Yes, the one already established: there is no frictional force.