yecko
Gold Member
- 275
- 15
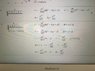
Homework Statement
Homework Equations
Beam problem
Deflection
Statically indeterminate
The Attempt at a Solution
Am I correct? Or should the assumed deflection at B be the difference in deflection between B and C? Thanks