manan1
- 7
- 0
PROBLEM 1

The frame in the figure is supported by a hinge in A and a roller in G. It is loaded by a couple = 14 kN*m in B, a force = 12 kN in D and a distributed force = 4 kN/m on section EG. = 1.4 m.
Calculate the normal force in C. Use the correct signs for tension and compression. Hint: Solve using the principle of virtual work and use previously mastered methods to check your answer.
This is a problem from mastering engineering, the statics book. I can solve the problem using equilibrium equations, but i want to know what i am doing wrong with when I am doing using the virtual work theorem.
\deltaW = 0
\delta\theta small → tan ( \delta\theta) ≈ \delta\theta ;

\delta\theta_{1} = \delta\theta_{2} = \delta\theta
\delta\theta_{1} = \delta u_{1}/a
\delta\theta_{2} = \delta u_{2}/2a
LET
\delta u_{2} = \delta u
\delta u_{2}/2a = \delta u_{1}/a → \delta u_{1} = \delta u/2
\delta u_{3}/(a/2) = \delta u/2a → \delta u_{3} = \delta u/4
\delta u_{5} = \delta u_{1} = \delta u/2
\delta u_{4} = \delta u_{2} = \delta u
\delta W = 0
Therefore
-M*\delta\theta-N*\delta u_{5}-N*\delta u_{4}-F*\delta u_{2}-qa*\delta u_{3} = 0
\delta u ≠ 0
-M*\delta u/2a-N*\delta u/2-N*\delta u-F*\delta u-qa*\delta u/4 = 0
-\frac{3}{2}N = M/2a + F + qa/4
N = -12.2666... kN
But the answer should be -17.6 kN according to equilibrium equations.
PROBLEM 2
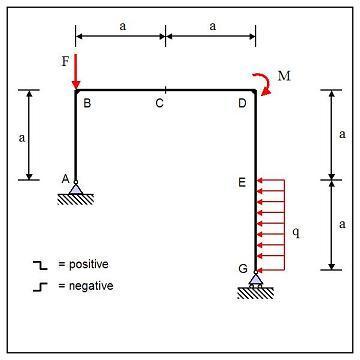
The frame in the figure is supported by a hinge in A and a roller in G. It is loaded by a couple = 4 kN*m in D, a force = 6 kN in B and a distributed force = 1 kN/m on section EG. = 1.5 m
Calculate the shear force in C with the sign convention as shown in the figure. Hint: Solve using the principle of virtual work and use previously mastered methods to check your answer.
\deltaW = 0
\delta\theta small → tan ( \delta\theta) ≈ \delta\theta ;
I have no idea how to calculate the virtual displacement for the force F at B.
Homework Statement
The frame in the figure is supported by a hinge in A and a roller in G. It is loaded by a couple = 14 kN*m in B, a force = 12 kN in D and a distributed force = 4 kN/m on section EG. = 1.4 m.
Calculate the normal force in C. Use the correct signs for tension and compression. Hint: Solve using the principle of virtual work and use previously mastered methods to check your answer.
This is a problem from mastering engineering, the statics book. I can solve the problem using equilibrium equations, but i want to know what i am doing wrong with when I am doing using the virtual work theorem.
Homework Equations
\deltaW = 0
\delta\theta small → tan ( \delta\theta) ≈ \delta\theta ;
The Attempt at a Solution
\delta\theta_{1} = \delta\theta_{2} = \delta\theta
\delta\theta_{1} = \delta u_{1}/a
\delta\theta_{2} = \delta u_{2}/2a
LET
\delta u_{2} = \delta u
\delta u_{2}/2a = \delta u_{1}/a → \delta u_{1} = \delta u/2
\delta u_{3}/(a/2) = \delta u/2a → \delta u_{3} = \delta u/4
\delta u_{5} = \delta u_{1} = \delta u/2
\delta u_{4} = \delta u_{2} = \delta u
\delta W = 0
Therefore
-M*\delta\theta-N*\delta u_{5}-N*\delta u_{4}-F*\delta u_{2}-qa*\delta u_{3} = 0
\delta u ≠ 0
-M*\delta u/2a-N*\delta u/2-N*\delta u-F*\delta u-qa*\delta u/4 = 0
-\frac{3}{2}N = M/2a + F + qa/4
N = -12.2666... kN
But the answer should be -17.6 kN according to equilibrium equations.
PROBLEM 2
Homework Statement
The frame in the figure is supported by a hinge in A and a roller in G. It is loaded by a couple = 4 kN*m in D, a force = 6 kN in B and a distributed force = 1 kN/m on section EG. = 1.5 m
Calculate the shear force in C with the sign convention as shown in the figure. Hint: Solve using the principle of virtual work and use previously mastered methods to check your answer.
Homework Equations
\deltaW = 0
\delta\theta small → tan ( \delta\theta) ≈ \delta\theta ;
The Attempt at a Solution
I have no idea how to calculate the virtual displacement for the force F at B.
Attachments
Last edited: