TimChoi89
- 3
- 0
Homework Statement
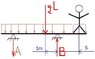
The uniform work platform, which has a mass per unit length of 28kg/m, is simply supported by cross rods A and B the 90-kg construction worker starts from point B and walks to the right. At what location S will the combined moment of the weights of the man and platform about point B be zero?
Platform illustration:
__A____________B___man (going to the right)___
Mass per unit length of bridge: 28kg/m
Mass of man: 90kg
Distance from far left end of bridge to A: 1m
Distance between A and B: 4m
Distance from B to far right end of bridge: 3m
Distance from B to man: S
Homework Equations
M=d*F or M=r*F (cross product)
The Attempt at a Solution
What I did was that I set point B to be (0,0) so any distances to the left of B is (-) and to the right will be (+). Also, I set all the weights to be (-) since it's going down the (-) y-axis.
Next I assigned the F from B to Man to be (90+28S) and the F from B to the remaining distance from Man to far right end of the bridge to be 28(3-S).
For the forces on the left side:
left end to A: 28
between A and B: 112
Next, I used M=d*F and set the moment of B from the left and right side to equal each other which leaves me with:
588=-90S-28S^2+(3-S)(-8.4+28S)
840=78S-56S^2
0=78S-56S^2-840
0=9.8(78S-56S^2-840) <-- to calculate weight
0=548.8S^2-764.4S+8232
When I try to solve for S, I use the quadratic formula but I can't solve for S because the number in the sqrt is (-) thus I can't solve for S. Am doing something wrong with the signs or is my approach completely wrong? Thanks for your help!