jklops686
- 39
- 0
Statics Springs "Design Problem"
Here's a problem I've been very determined to figure out, but I can't. I attached the picture. This single problem is 5% of my grade, so I'd appreciate any help!
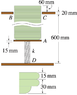
A plate storage system for a self-serve salad bar in a restaurant is shown. As plates are added to or withdrawn from the stack, the spring force and stiffness are such that the plates always protrude above the tabletop by about 60 mm. If each plate has 0.509 kg mass, and if the support A also has 0.509 kg mass, determine the stiffness k and unstretched length L0 of the spring. Assume the spring can be compressed by a maximum of 40% of its initial unstretched length before its coils begin to touch. Also specify the number of plates that can be stored. Assume the system has guides or other mechanisms so the support A is always horizontal.
Spring force=stiffness*(L-Lo) L=final elongation and Lo=initial elongation
There's 3 parts to the spring equation and I can only get one by a random number of plates (since you can't tell how many exactly their are in the picture) and taking their weight force. By summing the forces in the y direction i get Force of spring-mg=0, so Fs=mg. That's what I tried and got me...nowhere. I'm guessing I should find the stiffness first since it's listed first in the problem statement, but I'm not sure how to, or what to use for elongation.
Homework Statement
Here's a problem I've been very determined to figure out, but I can't. I attached the picture. This single problem is 5% of my grade, so I'd appreciate any help!
A plate storage system for a self-serve salad bar in a restaurant is shown. As plates are added to or withdrawn from the stack, the spring force and stiffness are such that the plates always protrude above the tabletop by about 60 mm. If each plate has 0.509 kg mass, and if the support A also has 0.509 kg mass, determine the stiffness k and unstretched length L0 of the spring. Assume the spring can be compressed by a maximum of 40% of its initial unstretched length before its coils begin to touch. Also specify the number of plates that can be stored. Assume the system has guides or other mechanisms so the support A is always horizontal.
Homework Equations
Spring force=stiffness*(L-Lo) L=final elongation and Lo=initial elongation
The Attempt at a Solution
There's 3 parts to the spring equation and I can only get one by a random number of plates (since you can't tell how many exactly their are in the picture) and taking their weight force. By summing the forces in the y direction i get Force of spring-mg=0, so Fs=mg. That's what I tried and got me...nowhere. I'm guessing I should find the stiffness first since it's listed first in the problem statement, but I'm not sure how to, or what to use for elongation.