Streamlines around a sphere (qualitative)

  • I
  • Thread starter member 428835
  • Start date
  • Tags
    Sphere
In summary, the conversation discusses the difference in spacing of streamlines in a figure from Bird Stuart and Lightfoot. The interpretation is that the difference between streamlines represents volumetric flow rate, and closer streamlines indicate faster flow. However, it is pointed out that the figures may not accurately represent the actual streamlines. It is also noted that the distance in physical space between streamlines is meaningless unless the inflow is constant, and that equal delta y does not always indicate equal Q. The conversation concludes with the statement that in this system, equal delta y identifies equal Qs far upstream and downstream.
  • #1
member 428835
Hi PF!

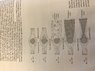
Attached is an figure from Bird Stuart and Lightfoot. I'm wondering if anyone can comment about the difference in spacing of these streamlines assuming each streamfunction is evenly spaced (or does this requirement make this picture invalid)?

My interpretation assuming each streamfunction sketched is evenly spaced, meaning ##\psi = 1,2,3...##: the difference between any two streamfunctions is volumetric flow rate. Then streamlines closer together would imply faster flow, so that the flow is the fastest in the far field before and after the solid body in figures a, b, that flow is fastest before the solid body in figures c and d, and that flow is fastest close to the solid body in figure e. Assuming the streamfunctions are evenly spaced, is this interpretation true?
 

Attachments

  • IMG_3941.JPG
    IMG_3941.JPG
    76.2 KB · Views: 423
Physics news on Phys.org
  • #2
Your interpretation is correct, but it seems to me that the figures are only schematic, and don't represent plots of the actual streamlines.
 
  • Like
Likes BvU
  • #3
Thanks, I was thinking the same!
 
  • #4
I'd also like to point out that the distance in physical space between steamlines is meaningless unless the inflow is constant. It's the distance in ##\psi## space that matters. Two pairs of streamlines can both originate ##\Delta y## apart from each other, but they still may not have the same ##Q## between them.
 
  • Like
Likes member 428835
  • #5
Totally! This is an important point boneh3ad.
 
  • #6
boneh3ad said:
I'd also like to point out that the distance in physical space between steamlines is meaningless unless the inflow is constant. It's the distance in ##\psi## space that matters. Two pairs of streamlines can both originate ##\Delta y## apart from each other, but they still may not have the same ##Q## between them.
In this system, far upstream and far downstream, equal delta y identify equal Qs.
 
  • #7
Chestermiller said:
In this system, far upstream and far downstream, equal delta y identify equal Qs.

Sure, but that's not a general rule.
 

FAQ: Streamlines around a sphere (qualitative)

1. What is the purpose of studying streamlines around a sphere?

The purpose of studying streamlines around a sphere is to understand the flow of a fluid (such as air or water) around a solid object. This can help in the design of aerodynamic or hydrodynamic structures, as well as in predicting the behavior of fluids in various situations.

2. How are streamlines around a sphere visualized?

Streamlines around a sphere can be visualized using a technique called flow visualization, where a dye or particles are introduced into the fluid and their movement is observed. Alternatively, computer simulations can also be used to generate a visual representation of the streamlines.

3. What factors influence the shape and distribution of streamlines around a sphere?

The shape and distribution of streamlines around a sphere are influenced by several factors, including the shape and size of the sphere, the velocity of the fluid, and its viscosity. Other factors such as the surface roughness of the sphere and the presence of other objects in the flow can also affect the streamlines.

4. Why do streamlines around a sphere converge at the back of the sphere?

Streamlines around a sphere converge at the back of the sphere because of the phenomenon known as the Coanda effect. This occurs when a fluid follows the curvature of a surface, resulting in a change in direction of the flow. In the case of a sphere, the flow is diverted towards the back of the sphere, causing the streamlines to converge.

5. How are streamlines around a sphere related to lift and drag forces?

The streamlines around a sphere are closely related to the lift and drag forces experienced by the sphere. The distribution and shape of the streamlines can give insight into the magnitude and direction of these forces. For example, a larger separation of streamlines at the back of the sphere indicates a higher drag force, while a curved streamline at the top of the sphere can indicate a lift force.

Similar threads

I How to understand experiment to measure heat capacity of solid?
Replies
1
Views
974
Rotating Sphere: Conceptual Question
Replies
10
Views
2K
I Band theory and qualitative character of bands
Replies
4
Views
2K
Buoyancy: Archimedes' Wooden Spheres
Replies
1
Views
3K
What factors affect heat rejection in vacuum pump systems?
Replies
3
Views
2K
I How weather conditions affect a golf shot
Replies
6
Views
2K
Effect of density on downward rolling spheres
Replies
14
Views
3K
I Compressible choked gas flow through an orifice -- Excel formula
Replies
1
Views
2K
Theoretical Fluid Mechanics - Ideal Fluid Flow
Replies
4
Views
4K
I Are Tidal Forces Curvature of Space?
Replies
9
Views
2K

Hot Threads

Recent Insights

Back
Top