sthoriginal
- 9
- 0
Hi. I have a huge problem and without solving it I can't move forward. I will appreciate any help.
Having the stress tensor S:
163.666557052527 -63.0272557558942 0.000000000000000E+000
-63.0272557558942 70.3802282767392 0.000000000000000E+000
0.00000000000000 0.00000000000000 0.000000000000000E+000
σ11 - North, σ22 - East, σ33 - Down
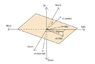
I have to calculate the normal stress and shear stress in slip direction for this focal mechanism
α - strike = 315°, β - dip = 73°, and λ - rake(slip) = 55°.
I think I know how to calculate the normal stress but I have no idea how to compute the shear stress in slip direction (55°)
Please help!
M.
Having the stress tensor S:
163.666557052527 -63.0272557558942 0.000000000000000E+000
-63.0272557558942 70.3802282767392 0.000000000000000E+000
0.00000000000000 0.00000000000000 0.000000000000000E+000
σ11 - North, σ22 - East, σ33 - Down
I have to calculate the normal stress and shear stress in slip direction for this focal mechanism
α - strike = 315°, β - dip = 73°, and λ - rake(slip) = 55°.
I think I know how to calculate the normal stress but I have no idea how to compute the shear stress in slip direction (55°)
Please help!
M.