Stuck on a single loop circuit, two emfs and resistor

[scrilla103]

Homework Statement

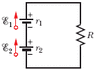
ε[1]=12v
internal resistance[1]=.016Ω
ε[2]=12v
internal resistance[2]=.012Ω

some unknown resistance 'R' in a stand alone resistor.

a) what value of 'R' will make the terminal-to-terminal potential difference of one of the batteries zero?
b) which battery would it be?
(picture below shows circuit)

Homework Equations

R = V/i

The Attempt at a Solution

I put together this equation:
ε[2] - ir[2] + ε - ir[1] - iR = 0
and continued to simplify to this:
i(.028 + R) = 24
The problem is I don't have a way to find 'i'...
Any ideas? This problem is marked as a three dot (harder difficulty) in my book, so I'm guessing there's an assumption I'm missing.

Thanks in advance,
Caleb

 

[skeptic2]

What would short circuit current be, i.e. R = 0?

 

[rude man]

Why solve for i?

What is the equation for voltage across E₁ to be zero? E₂?

Could you come up with 2 equations with 2 unknowns (i and R) for either of those?

 

[scrilla103]

Alright, I think I got it.

I set V₁ = ε₁ - ir₁ = 0
and got ε₁ = ir₁
and also
ε₂ = ir₂

Subbing 'i' into the equation I had simplified to above produces, for emf #1, I get R to equal .004Ω (which is what the back of the book says). Doing the same for emf #2, I get -.004Ω.

My only question now is about the negative. Doesn't a negative value on a resistor mean it encourages the flow of charge? Wouldn't that mean that the battery set to zero potential could be either one, just depending on the sign of R? (The book says battery one is the answer to part b.)

Thanks,
Caleb

 

[rude man]

For you, there is no such thing as a negative resistor, certainly not a dc negative resistor. So your only valid solution is for E1.

You've run into this sort of thing many times before, even in high school. For example, Pythagoras says c^2 = a^2 + b^2. But that equation has two solutions for c, and you know one of them is nonsensical.