Stuck on an Electrical Potential Energy Question

[Nathan phisi]

Homework Statement

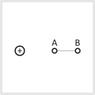
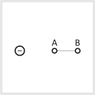
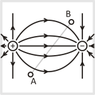
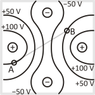
A charge of Q = −1 µC is moved from point A to point B.

Which of the following situations will result in an increase in electrical potential energy?
I've now uploaded the files below

Homework Equations

F = qE
U = qV
a

b

c

d

e

f

g

h

The Attempt at a Solution

I think an increase in electrical potential energy requires work to move the charge from a to b.
I guess a is one correct answer because the negative charge moves closer to another and they are repelling each other.
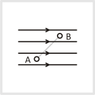
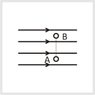
I think the negative charge experiences a force opposite to the electric field, so c is one, and maybe e. But that's all I can get. Some help understanding would be greatly appreciated :)

 

[Arman777]

Which of the following situations will result in an increase in electrical potential energy?

If you think two plates then electric field between them will be uniform.So If we put a positive charge on the positively charged side it will move to negative side of the plate.So potential difference is negative and potential energy difference is also negative (In this motion)

So If a charge moves in the direction of electric field its potential decreases (or potential energy). If we generalize this we get $ΔV=-\int \vec E⋅d\vec r$ (Eqn.1)so In this case question asks us increase in electric potential energy then using the above equation we can conclude about the motion.
Remember this, $ΔU=qΔV$ you want to $ΔU$ be positive.
Be carefull about the vectors.
You can obtain (Eqn.1) using $W=\int \vec F⋅d\vec r$ and $W=-ΔU$ and $ΔU=qΔV$

 

[kuruman]

So If a charge moves in the direction of electric field its potential decreases (or potential energy).

This statement is misleading. First, potential is not a property of a charged particle, but a property of space. It is the potential energy per unit positive charge. If I place a 1 C charge at a point in space where the electric potential is -5 V, the charge's potential energy will be - 5 J; if I place a -1 C instead, its potential energy will be +5 J but the potential at that point is still - 5 V. So it is misleading to talk about a charge's potential. Second, only positively charged particles that move in the direction of the electric field decrease their potential energy; negatively charged particles increase their potential energy when they move in the direction of the electric field. Here, the particle is negatively charged.

 

[ehild]

Homework Statement

A charge of Q = −1 µC is moved from point A to point B.

Which of the following situations will result in an increase in electrical potential energy?

Keep in mind that the potential energy of a point charge Q at a point in an electric field is QU where U is the potential at the point. As Q is negative, the potential energy of the charge is higher in the point where the potential is lower: QU_B > QU_A if U_B<U_A.

 

[Arman777]

This statement is misleading. First, potential is not a property of a charged particle, but a property of space. It is the potential energy per unit positive charge. If I place a 1 C charge at a point in space where the electric potential is -5 V, the charge's potential energy will be - 5 J; if I place a -1 C instead, its potential energy will be +5 J but the potential at that point is still - 5 V. So it is misleading to talk about a charge's potential. Second, only positively charged particles that move in the direction of the electric field decrease their potential energy; negatively charged particles increase their potential energy when they move in the direction of the electric field. Here, the particle is negatively charged.

Lets think a two points in space.One location potential is 0 and other one -5V.Then If we have a positive particle it will move towards the -5V side right ? So Its last potential energy +q(-5V-0V)=-5j

Same points but we have a negative charge.Negative charge moves towards the 0 potential point in this case (Due to electric field, force acts on that direction).So -q(0V-(-5)V)=-5j potential is decreased.

We can only define potential differences hence potential energy differences.