rwooduk
- 757
- 59
Mentor note: fixed formulas so they get displayed properly
If we take the K-G eqn and the following term for the wave function
$$( \partial^2 + \frac{m^{2}c^{2}}{\hbar^{2}})\Psi =0
\\\\\Psi = Re^{-i\omega t + i k_{i}x_{i}}$$We worked through to this ##\hbar \omega = \pm \sqrt{\hbar^{2} c^{2}k_{i}k_{i}+ m^{2}c^{4}}## which is fine and recognisable, but I can't get the ##\hbar^{2} c^{2}k_{i}k_{i}## term to equal the familiar ##\rho^{2}c^{2}##. I'm assuming it's obvious and that's why he didnt show it, but I'm a bit stuck.
Any help would be appreciated.
edit
he also did something similar here:
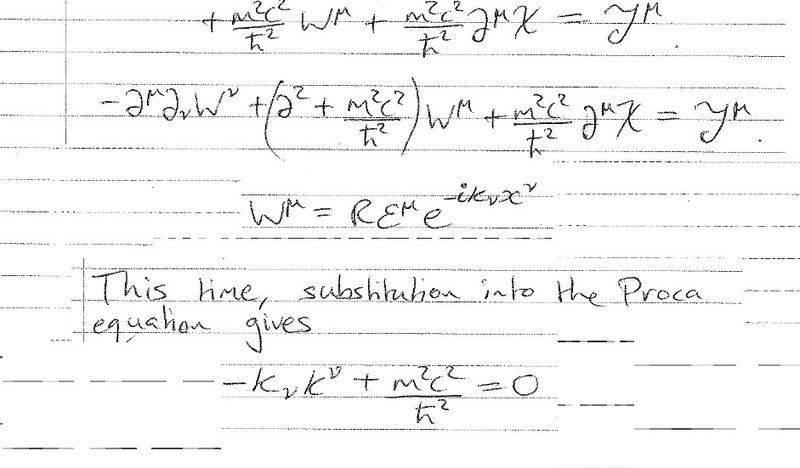
If we take the K-G eqn and the following term for the wave function
$$( \partial^2 + \frac{m^{2}c^{2}}{\hbar^{2}})\Psi =0
\\\\\Psi = Re^{-i\omega t + i k_{i}x_{i}}$$We worked through to this ##\hbar \omega = \pm \sqrt{\hbar^{2} c^{2}k_{i}k_{i}+ m^{2}c^{4}}## which is fine and recognisable, but I can't get the ##\hbar^{2} c^{2}k_{i}k_{i}## term to equal the familiar ##\rho^{2}c^{2}##. I'm assuming it's obvious and that's why he didnt show it, but I'm a bit stuck.
Any help would be appreciated.
edit
he also did something similar here:
Last edited: