DerekBrown
- 13
- 0
I've currently got a quick and short question about making something the subject of the formula. I've managed to do most of it myself, I'm just stuck on the last bit.
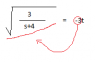
Here is a picture of what I've got so far, how do I make 't' the subject of the formula?
Here is a picture of the formula: http://puu.sh/7chNU.jpg
Thanks!
Here is a picture of what I've got so far, how do I make 't' the subject of the formula?
Here is a picture of the formula: http://puu.sh/7chNU.jpg
Thanks!
Last edited by a moderator: