wirefree
- 110
- 21
I appreciate the opportunity afforded by this forum to submit a question.
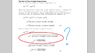
I have struggled with the derivation shown in the attached picture. I am certainly unfamiliar with the concept used to include the arctan function in the encircled step.
Would be highly appreciative of a prompt.wirefree
I have struggled with the derivation shown in the attached picture. I am certainly unfamiliar with the concept used to include the arctan function in the encircled step.
Would be highly appreciative of a prompt.wirefree