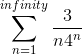Kqwert
- 160
- 3
Homework Statement
Find the sum of the series
Homework Equations
The Attempt at a Solution
Not sure exactly where to start. If I move 3 outside the sum I'm left with 3*sigma(1/n*4^n), which I can rewrite to 3*sigma((1/n)*(1/4)^n), which party looks like a geometric series..Any tips?