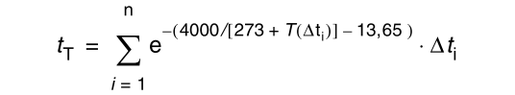Cokemaster
- 9
- 0
Hello,
Some of you may know this equation and I need help solving it.
Delta ti is the time in days at a certain temperature (0 - 80).
T(Delta ti) is the temperature during Delta ti.
The answer is supposed to be an age in days but my tries have given me answers that are below 1, which doesn't make any sense. Can someone please try to open this up for me?
Some of you may know this equation and I need help solving it.
Delta ti is the time in days at a certain temperature (0 - 80).
T(Delta ti) is the temperature during Delta ti.
The answer is supposed to be an age in days but my tries have given me answers that are below 1, which doesn't make any sense. Can someone please try to open this up for me?