Virous
- 68
- 0
I have a question about, perhaps, GCSE level physics, if not below, which, for some reason, is not explained anywhere I've looked up. Or, at least, I didn't find any explanation.
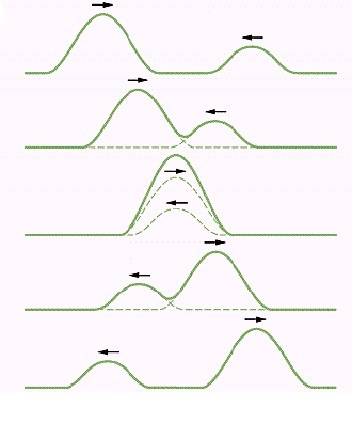 The picture above is supposed to explain the concept of superposition. It depicts a pair of one-dimensional waves (wave pulses) at 5 different points in time. On the third picture (the exact moment of superposition), the initial individual waves do not exist. Instead we have a single large wave, composed of the energy of both. Where is the information about the shapes of the initial waves at this moment of time stored?
The picture above is supposed to explain the concept of superposition. It depicts a pair of one-dimensional waves (wave pulses) at 5 different points in time. On the third picture (the exact moment of superposition), the initial individual waves do not exist. Instead we have a single large wave, composed of the energy of both. Where is the information about the shapes of the initial waves at this moment of time stored?
In other words, after the third picture, how does this large wave "know" how it should split in order to restore the initial pulses?
Thank you!
In other words, after the third picture, how does this large wave "know" how it should split in order to restore the initial pulses?
Thank you!