Tom Hammer
- 12
- 2
- Homework Statement
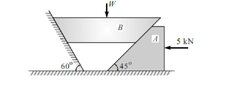
- Find the weight W that can be supported by the applied force of 5 kN. Mu = .25 at all surfaces
- Relevant Equations
- F = mu N, where mu = coefficient of static friction, N = normal force
Let Nr = normal force on the right side of the trapezoid B and Fr = the force of friction on the right side of B.
Let Nl = normal force on the left side of B and Fr = the frictional force on the left surface of B
so Nr = 5 sin45 and Fr = 5 sin45 =
and Nl = 5 sin 60, Fl = 5 sin 30.
Let Nl = normal force on the left side of B and Fr = the frictional force on the left surface of B
so Nr = 5 sin45 and Fr = 5 sin45 =
and Nl = 5 sin 60, Fl = 5 sin 30.