Suppose that three astronomical objects

  • Thread starter MakeItThrough
  • Start date
In summary, studying three astronomical objects can help us understand their relationships and interactions, as well as provide insights into the larger structures and systems of the universe. Scientists use methods such as telescopes, satellites, and data analysis to study these objects, and determine their distance using techniques like parallax and redshift. By studying three astronomical objects, scientists can gather information about their composition, size, mass, temperature, and movement, and gain insights into the origins and fate of the universe.
  • #1
MakeItThrough
13
0

Homework Statement


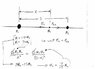
Suppose that three astronomical objects (1, 2, and 3) are observed to lie on a line, and that the distance from object 1 to object 3 is D. Given that object 1 has 1.5 times the mass of object 3 and seven times the mass of object 2, find the distance (in terms of D) between objects 1 and 2 for which the net force on object 2 is zero.
____ D m


Homework Equations


F = (G x m1 x m2) / r^2


The Attempt at a Solution


I drew a diagram of this, and had no luck figuring out what to do next.
 
Physics news on Phys.org
  • #2


Does this help?
 

Attachments

  • masses081.jpg
    masses081.jpg
    22.4 KB · Views: 1,472

What is the significance of studying three astronomical objects?

Studying three astronomical objects can help us understand the relationship between these objects and how they interact with each other. It can also provide insights into the larger structures and systems of the universe.

What methods are used to study three astronomical objects?

Scientists use a variety of methods to study three astronomical objects, including telescopes, satellites, and spacecraft. They also use data analysis techniques and computer simulations to gather and analyze information.

How do scientists determine the distance between three astronomical objects?

Scientists use various techniques such as parallax, redshift, and the cosmic distance ladder to determine the distance between three astronomical objects. They can also use the objects' apparent brightness and known properties to calculate their distance.

What types of information can be gathered from studying three astronomical objects?

Studying three astronomical objects can provide information about their composition, size, mass, temperature, and movement. It can also help us understand their formation and evolution over time.

What can the study of three astronomical objects tell us about the universe?

By studying three astronomical objects, scientists can gain insights into the larger structures and systems of the universe, such as galaxies, clusters, and superclusters. It can also help us understand the origins and fate of the universe.

Similar threads

Particle dynamics (mechanics): inclined plane, pulley, two blocks
    • Introductory Physics Homework Help
Replies
14
Views
954
How to find the equilibrium position of three masses (two of them fixed)?
    • Introductory Physics Homework Help
Replies
4
Views
887
Distance between rocket and object
    • Introductory Physics Homework Help
Replies
30
Views
2K
Acceleration in a pulley system
    • Introductory Physics Homework Help
Replies
8
Views
6K
Finding the center of mass of a homogeneous object
    • Introductory Physics Homework Help
Replies
6
Views
3K
What is the intersection point of two objects on a position vs time graph?
    • Introductory Physics Homework Help
Replies
10
Views
1K
3 pulley problem with attached masses
    • Introductory Physics Homework Help
Replies
15
Views
2K
Why does the gravitational force decrease below the Earth's surface?
    • Introductory Physics Homework Help
Replies
10
Views
2K
Object causing another object to move with zero friction
    • Introductory Physics Homework Help
Replies
3
Views
1K
Finding shortest distance between an observer and a moving object
    • Introductory Physics Homework Help
Replies
13
Views
738

Hot Threads

Recent Insights

Back
Top