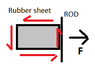
I will leave the explanation due to energy arguments here:
The work done in keeping the film at its current position is F x d where d is the horizontal length of the film (from the left to the right). The surface energy is equivalent to the surface tension, multiplied by the surface area of the liquid film, which in this case, is the horizontal length, multiplied by the vertical length.
If it is assumed all the applied work is acting to create the surface (in reality some energy is lost to friction on the frames), then:
Fd = 2σ dA = 2σdL
The factor of two accounts for the fact that there are two surfaces. Thus, the d's are canceled and the subsequent equation is σ = F / 2L. This allows you to calculate the surface tension of a liquid with a known applied force, and known dimensions of a frame, if it is assumed frictional effects are negligible.
Sources:
Cengel and Cimbala - Fluid Mechanics Fundamentals and Applications (Mechanical Engineering) (3rd edition)
Section 3.2.1 Surface Tension of Pure Liquids
Wakeham, W., et al., Material Properties: Measurement and Data, in Springer Handbook of Experimental Fluid Mechanics, C. Tropea, A.L. Yarin, and J.F. Foss, Editors. 2007, Springer Berlin Heidelberg. p. 85-177.
I also have several sources that say the surface tension acts parallel to a surface:
http://aapt.scitation.org/doi/abs/10.1119/1.3619866?journalCode=ajp
http://iopscience.iop.org/article/10.1088/0031-9120/6/2/001/meta
Physics vol 2 - Sunil Batra Section 19.9.2 (free preview is available on google books)
An Introduction to Fluid Dynamics - Batchelor (pg 61) (The passage here will be understood using the diagram in Sunil's book) (free preview is available on google books).
I would also refer people to the discussions here:
https://physics.stackexchange.com/questions/150836/why-is-surface-tension-parallel-to-the-interface
I think Orodruin's explanation, though it was not clear at the time, becomes clearer by imagining the liquid film is quite literally on the plane of the webpage (or book). Another way to look at it, is to imagine we are looking directly
on top of the liquid film. So imagine you have a glass of water, and you are literally looking into the glass of water onto the surface. That is the viewpoint.
Thus the applied force is acting
tangential to the surface of the film (remembering we are looking from the top, down onto the film). The surface tension force opposes this action by generating an equal but opposite force, tangential to the surface and also within the plane of the paper, thus the system is in a state of equilibrium. The value of the surface tension is constant, but the opposing force generated is larger because the area has increased and the surface tension force is defined as surface tension multiplied by length.
If the applied force is removed, the film moves to the left, whereby the film uses the least amount of energy to maintain its state of equilibrium.
PS: The liquid film remains attached to the sliding rod because of adhesion forces.
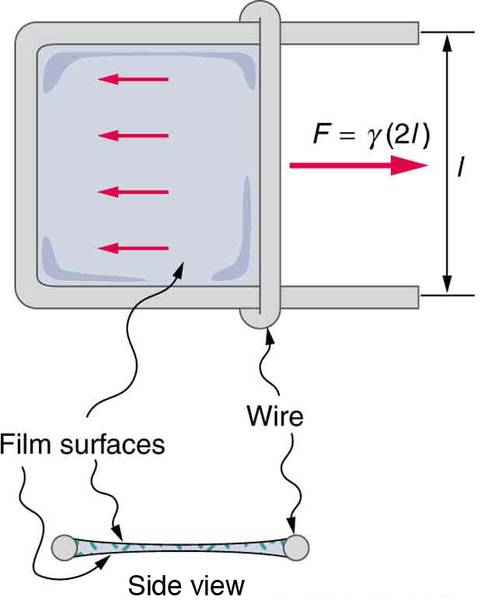 I understand that there are two surfaces to overcome, hence the factor of 2, but why is the length perpedicular to the force used and not the length parallel to the force, since surface tension is defined as the force parallel to a surface per unit length of that surface??
I understand that there are two surfaces to overcome, hence the factor of 2, but why is the length perpedicular to the force used and not the length parallel to the force, since surface tension is defined as the force parallel to a surface per unit length of that surface??