fire765
- 4
- 0
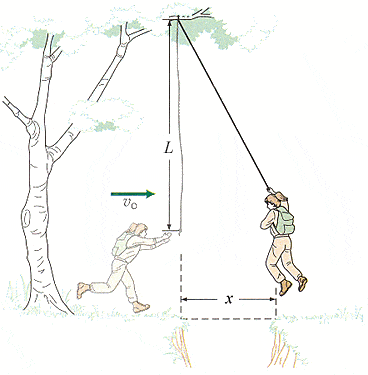
A hiker plans to swing on a rope across a ravine in the mountains, as illustrated in the figure, where L = 4.9 m and x = 2.7 m, and to drop when she is just above the far edge. At what minimum horizontal speed should she be moving when she starts to swing(in m/s)?
I tried using the equation for range (x=(vo^2sin2(angle))/g but it didnt work, and I am guessing I am on the complete wrong track.
I tried using the equation for range (x=(vo^2sin2(angle))/g but it didnt work, and I am guessing I am on the complete wrong track.