- 1,255
- 143
I have often thought about how the one-way speed of light can be measured without having to use synchronized clocks, which tends to be controversial because the clocks are normally synchronized by using one-way light in the first place. Recently, Don Lincoln of Fermi-Lab suggested a method to me. To convince myself, I tested it in a thought experiment, using two clocks and two cables in a frame that is boosted by accelerating it to a new inertial frame. I thought it useful to share it and get other opinions.
First, Don Lincoln's test.
I expanded Don's test as follows:
Consider two spaceships connected by a taut cable of 600 units long. Add Don’s second identical cable, folded back and strapped at the half-distance point (for ease of presentation) so that the setup becomes equivalent to his scenario, with the cables calibrated for identical transmission times. Accelerate the whole ‘lab’ lengthwise to 0.6c in such a way that the cables do not stretch (Born-rigidity) and let it coast again.
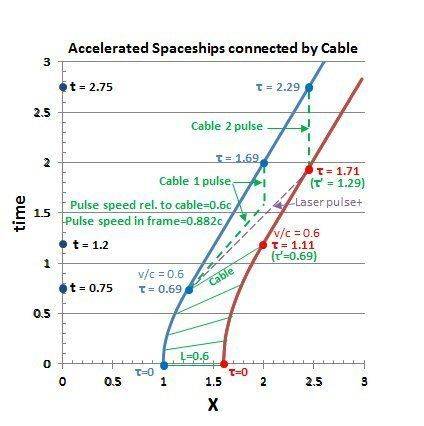
I used the Rindler coordinates equation t = \sqrt{x^2-\sigma^2}, where \sigma is the distance of the start of the curve from the origin (1 and 1.6 units respectively). The origin coincides with the common light cone of Rindler observers with constant proper acceleration (a), where a =1 / \sigma. The other relevant equations are: \tau = \sigmaasinh(a t) and v/c = tanh(a \tau).
The spacetime diagram is a tad busy, but gives an overview of all the values calculated for the acceleration phase and the later cruise phase.
Click on the thumbnail below if you do not see the diagram.
For simplicity, use a cable with a signal speed of exactly 0.6c, so that a signal takes exactly one time unit to travel the length of the cable. After the acceleration, the speed of the pulse relative to the original reference frame is (0.6\pm0.6)/(1+0.36)c, i.e. 0.882c in the forward direction and zero in the return direction.
In the reference frame the acceleration lasts for t=0.75 units for the blue ship and t=1.2 units for the front ship. The corresponding ship proper times are \tau_{blue}=0.69 and \tau_{red}=1.11 units. The latter clock must be set back by 0.42 units to \tau'_{green}=0.69 units in order to be synchronized with blue again.
The pulse in cable 1 is transmitted simultaneously with the laser pulse and arrives back at the oscilloscope at \tau_{blue}=1.69, while the cable 2 pulse arrives at \tau_{blue}=2.29. This gives a time delay of 0.6 units, which is the travel time of the laser pulse. Since we expect the proper length of the cable to remain the same before and after acceleration, this seems to indicate that it is a true clock-sync-independent measurement of the one-way speed of light in an inertial frame. If correct, this also means that calibrated cables can be used to synchronize distant clocks without slow transport involved.
First, Don Lincoln's test.
Take two photon detectors. These can be arbitrarily thin - less than a millimeter if necessary. Take the two detectors and place them side by side. From each detector take a cable of a convenient length. Put both of those cables into fast electronics (a modern digital oscilloscope will work just fine).
Fire a light pulse through both detectors. Since these two detectors are adjacent to one another, the transit time from one to the other is of order (1 mm)/(speed of light) = (1 x 10-3 m)/(3 x 108 m/s) = 3 x 10-12 seconds. If sub- 3 picosecond speed is needed, there are ways.
Using your oscilloscope, you can calibrate your cables to establish what "simultaneous" means. In the abstract, the cables can be of identical length. This means that the signals from the two detectors will arrive simultaneously at your oscilloscope.
Now move one detector far away...maybe 1000 feet. Do not disconnect the cables, so you have identical conditions. Fire the light pulse (use a laser) through one detector to hit the other. The signals from the two detectors will transit the cables and hit your oscilloscope at a single spatial point. Since you have already established that the transit time in the cables of both detectors are identical, the only difference between the signal arrival time at your detector is the transit time of light from one to the other. If you have measured the distance exactly, you can then determine the speed of light by distance over time.
I expanded Don's test as follows:
Consider two spaceships connected by a taut cable of 600 units long. Add Don’s second identical cable, folded back and strapped at the half-distance point (for ease of presentation) so that the setup becomes equivalent to his scenario, with the cables calibrated for identical transmission times. Accelerate the whole ‘lab’ lengthwise to 0.6c in such a way that the cables do not stretch (Born-rigidity) and let it coast again.
I used the Rindler coordinates equation t = \sqrt{x^2-\sigma^2}, where \sigma is the distance of the start of the curve from the origin (1 and 1.6 units respectively). The origin coincides with the common light cone of Rindler observers with constant proper acceleration (a), where a =1 / \sigma. The other relevant equations are: \tau = \sigmaasinh(a t) and v/c = tanh(a \tau).
The spacetime diagram is a tad busy, but gives an overview of all the values calculated for the acceleration phase and the later cruise phase.
Click on the thumbnail below if you do not see the diagram.
For simplicity, use a cable with a signal speed of exactly 0.6c, so that a signal takes exactly one time unit to travel the length of the cable. After the acceleration, the speed of the pulse relative to the original reference frame is (0.6\pm0.6)/(1+0.36)c, i.e. 0.882c in the forward direction and zero in the return direction.
In the reference frame the acceleration lasts for t=0.75 units for the blue ship and t=1.2 units for the front ship. The corresponding ship proper times are \tau_{blue}=0.69 and \tau_{red}=1.11 units. The latter clock must be set back by 0.42 units to \tau'_{green}=0.69 units in order to be synchronized with blue again.
The pulse in cable 1 is transmitted simultaneously with the laser pulse and arrives back at the oscilloscope at \tau_{blue}=1.69, while the cable 2 pulse arrives at \tau_{blue}=2.29. This gives a time delay of 0.6 units, which is the travel time of the laser pulse. Since we expect the proper length of the cable to remain the same before and after acceleration, this seems to indicate that it is a true clock-sync-independent measurement of the one-way speed of light in an inertial frame. If correct, this also means that calibrated cables can be used to synchronize distant clocks without slow transport involved.
Attachments
Last edited:
