Resonant orbits have a mechanism that ensures their periods have perfect integer ratios.
Consider the following analogy. Two cars are on a circular one-lane track. If one of the cars is driving faster than the other, it will eventually catch up to the slower car, and be forced to slow down. It it slows down and becomes the slower car, the other car will eventually catch up, etc. At any moment, their periods might not be exactly 1:1, but over long periods of time it must average 1:1.
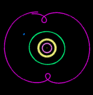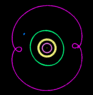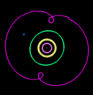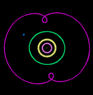
Now let's take the case of planets. In the following animation, Neptune is held stationary, and Pluto traces a 3:2 resonant pattern librating around Neptune. For every 3 orbits of the Sun completed by Neptune, Pluto completes 2 orbits. At any given moment, however, the ratio is not exactly 3:2. Sometimes Pluto's period is slightly faster than its average value. Sometimes it is slower.
When Pluto's period is slightly faster than average, the points where its orbit intersects the orbit of Neptune advance with each orbit. But when this intersection gets too close to Neptune, Pluto is accelerated by Neptune's gravity. This causes Pluto to rise into a higher orbit with a longer period. Now orbiting the Sun with a period slightly slower than its average value, the points where Pluto's orbit intersects Neptune's orbit retreat with each orbit. Eventually, it approaches Neptune from the other direction, allowing Neptune's gravity to pull Pluto into a lower orbit with a shorter period. This repeats indefinately, ensuring that Pluto and Neptune never get too close to each other.
Notice the orbit of Uranus (green). It is tracing a 2:1 pattern, but it is not eccentric enough to be locked into resonance. Its apogee is not close enough to Neptune to allow Neptune to significantly speed it up or slow it down. So this 2:1 pattern keeps advancing in the same direction rather than librating like Pluto.