sutupidmath
- 1,629
- 4
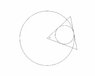
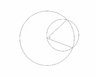
Problem: Given a circle of radius 1. Take a sector of this circle with internal angle A, where 0=<A=<pi/2. Find a formula for the radius of the smallest circle that will perfectly fit this sector, as a function of A.
Solution.
I used laws of sine and cosine and came up with:
R=\frac{\sqrt{2-2cos(A)}}{2sin(A)}.
So, i was wondering whether this is correct.
Basically, i thought this problem was equivalent to finding the radius of a circle circumscribing a given triangle. But i am not sure whether this is the right approach.
Thanks!
P.S. This is NOT a homework problem.
Solution.
I used laws of sine and cosine and came up with:
R=\frac{\sqrt{2-2cos(A)}}{2sin(A)}.
So, i was wondering whether this is correct.
Basically, i thought this problem was equivalent to finding the radius of a circle circumscribing a given triangle. But i am not sure whether this is the right approach.
Thanks!
P.S. This is NOT a homework problem.