123scope
- 4
- 0
Hi, I have a problem with this problem..
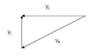
The figure (in the attachment) shows a bird's-eye view of a car going around a highway curve. As the car moves from point 1 to point 2, its speed doubles. Which vector shows the direction of the car's average acceleration between these two points?
Ok. According to my knowledge,
THe answer cannot be (g) and (b) and (a) is also unlikely
Applying the radial and tangential acceleration I guess it could be (d) and (f)
But I can't make my mind... Can anyine help me.
The figure (in the attachment) shows a bird's-eye view of a car going around a highway curve. As the car moves from point 1 to point 2, its speed doubles. Which vector shows the direction of the car's average acceleration between these two points?
Ok. According to my knowledge,
THe answer cannot be (g) and (b) and (a) is also unlikely
Applying the radial and tangential acceleration I guess it could be (d) and (f)
But I can't make my mind... Can anyine help me.